算法笔记

1.第一章 基础算法

时间复杂度

重视思想

好的方法 课下 模板(重复3-5次)思想理解会背 然后做题目

根据数据量猜解法

常数指令 一次a+b ,i ++这种就是，假如给你一个1e6长度的数组，用n^2的算法的话，数据量就成了1e12,我们设计的算法肯定不能超过1e7~1e8,假如用n*log2 n ，算下来也就是1e7多一点，未必能超，也许能行。假如是1e3长度，那么n2也行。

注意：上面使用技巧的必要条件↑

枚举

数对问题

https://leetcode.cn/problems/number-of-good-pairs/ 统计好数对

https://leetcode.cn/problems/count-number-of-bad-pairs/description/ 统计坏数对 双周赛80+

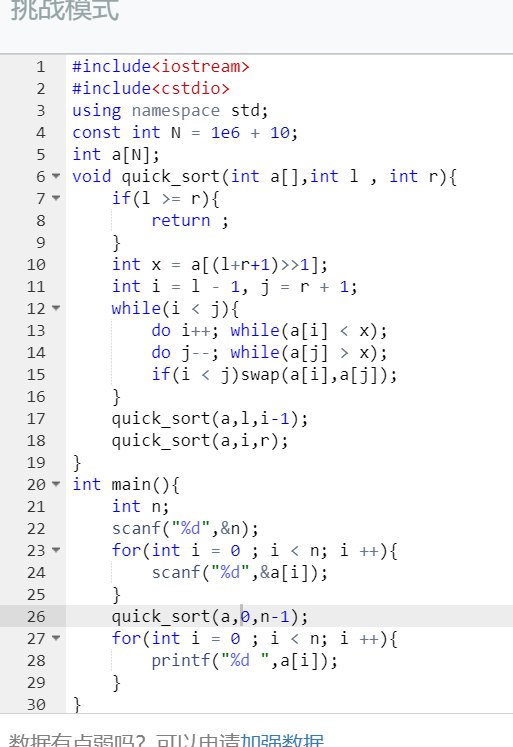
快速排序

用这个就行，防止边界问题

归并排序

思想也是分治,但是方法不一样

先划分区间，再合并

最后那个for是把temp拷贝回去 temp是记录递归排序的数组，每一步都在改变，不能最后直接输出temp

#include<iostream>
using namespace std;
int a[100010];
int t[100010];
/*void merge_sort(int a[],int l,int r){
    if(l == r)return;
    int mid = l + r >> 1;
    merge_sort(a,l,mid),merge_sort(a,mid+1,r);
    for(int i = l,j = l, k = mid + 1; i <= r; i ++){
        if(j == mid + 1) 
            t[i] = a[k ++];
        else if(k == r + 1)
            t[i] = a[j ++];
        else t[i] = a[j] < a[k] ? a[j ++] : a[k ++];
    }
    for(int i = l; i <= r; i ++)a[i]=t[i];
}*/
void merge_sort(int a[], int l, int r){
    //只剩一个元素的时候，已经有序，返回
    if(l >= r) return;

    //寻找数组中点下标
    int mid = (l+r)>>1;
    //递归给左半边排序
    merge_sort(a,l,mid);
    //递归给右半边排序
    merge_sort(a,mid+1,r);
    //以下是合并排序好的两个数组

    //k：遍历合并后的数组的下标
    int k = 0;
    //i:左半边数组的下标，j:右半边数组的下标
    int i = l, j = mid + 1;
    //左右半边都没遍历完
    while(i <= mid && j <= r){
        //左边的元素小于右边的元素
        if(a[i] < a[j]) 
            //左边元素放如临时数组，并移动下标
            temp[k++] = a[i++];
        //否则，右边元素放入临时数组并移动下标 
        else temp[k++] = a[j++];
    }
    //如果左边数组有剩余，则放入临时数组
    while(i <= mid) temp[k++] = a[i++];
    //如果有边数组有剩余，则放入临时数组
    while(j <= r) temp[k++] = a[j++];
    //把临时数组中的元素拷贝至原数组
    k = 0;
    for(int i = l; i <= r; i++){
        a[i] = temp[k++];
    }

}


int main(){
    int n;
    scanf("%d",&n);
    for(int i = 0 ; i < n; i ++){
        scanf("%d",&a[i]);
    }
    merge_sort(a,0,n-1);
    for(int i = 0 ; i < n; i ++){
        printf("%d ",a[i]);
    }
}

例题 逆序对

https://www.acwing.com/solution/content/5103/讲解很好

分治

计数排序

桶排序

例题洛谷P7020，适用情况，要排序的数字值域小，但是n很大的情况，sort和快排这些适合值域大小都可以，n小点的情况

二分

https://www.luogu.com.cn/problem/P6174

https://www.luogu.com.cn/problem/P5815 扑克牌[绿题] 二分答案

https://www.luogu.com.cn/problem/P1843 二分答案

https://www.acwing.com/solution/content/3338/ 数的范围讲解很好


#include <algorithm>
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int q[N];

int SL(int l, int r, int x) {
  while (l < r) {
    int mid = l + r >> 1;
    if (q[mid] >= x) r = mid;
    else l = mid + 1 ;
  }
  return l;
}

int SR (int l, int r, int x) {
  while (l < r) {
    int mid = l + r + 1 >> 1;
    if(q[mid] <= x) l = mid;
    else r = mid - 1;
  }
  return r;
}

int main() { int n,m;
    scanf ("%d%d",&n,&m);
    for(int i=0;i<n;++i) scanf ("%d",&q[i]);
    while ( m-- ) {
        int x;
        scanf ("%d",&x);
        int l = SL(0, n - 1, x);//查找左边界 并返回下标l
        if (q[l]!=x) cout <<"-1 -1"<<endl;//如果找不到  返回-1 -1
        else {
            cout << l << ' '; //如果找到了  输出左下标
            cout << SR(0, n - 1, x) << endl; //输出右下标
        }
    }
    return 0;
}
浮点数二分算法模板 —— 模板题 AcWing 790. 数的三次方根
bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

有经验，就是假如题目要求4位的话，最好-6，就是比要求的多两位，保证没问题

二分答案

lower_bound( )和upper_bound( )

https://blog.csdn.net/qq_40160605/article/details/80150252

例题 https://www.acwing.com/problem/content/732/

//可以用temp观察发现如果累加的和一直变大，不提前return,会导致负溢出
#include <iostream>
#include <cstdio>
using namespace std;
int n;
int maxH = -1;
int h[100005];
bool success(int x)
{
    int temp = x;
    for (int i = 1; i <= n; i++)
    {
        
        temp += temp - h[i];
        // cout <<"temp =="<<temp<<endl;
        if (temp < 0) return false;

        if (temp >= maxH) return true;
    }
    return true;
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &h[i]);
        maxH = max(maxH, h[i]);
    }
    int l = 0, r = maxH;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (success(mid))
        {
            r = mid;
        }
        else
        {
            l = mid + 1;
        }
    } 
    printf("%d\n", r);
    return 0;
}

例题 刺杀大使https://www.luogu.com.cn/problem/P1902

例题 路标设置 https://www.luogu.com.cn/problem/P3853 和跳石头基本一样（二分求最优解）

高精度（略过）

贪心

模板题

https://www.acwing.com/activity/content/problem/content/1763/

https://www.acwing.com/activity/content/problem/content/1764/

(很常见的板子题，取中位数)

https://www.matiji.net/exam/brushquestion/3/4347/179CE77A7B772D15A8C00DD8198AAC74

(用二分答案找时间，check部分贪心一下)

https://www.acwing.com/activity/content/problem/content/1766/
(y总思路很好)

https://www.acwing.com/activity/content/problem/content/1768/

https://www.acwing.com/problem/content/1226/

https://pintia.cn/problem-sets/994805342720868352/exam/problems/994805403651522560?type=7&page=0

https://pintia.cn/problem-sets/994805342720868352/exam/problems/994805350316752896?type=7&page=1

https://www.acwing.com/problem/content/127/ 耍杂技的牛（证明搞懂了！）

https://www.acwing.com/activity/content/problem/content/1111/ 区间选点(模板,搞懂和区间合并的区别)

https://www.acwing.com/activity/content/problem/content/1112/ 和上面区间选点一样

https://www.acwing.com/solution/content/5749/ 这个文章讲得不错

https://www.acwing.com/activity/content/problem/content/1113/ 区间分组 （类比活动安排)

https://www.acwing.com/solution/content/8902/上题题解，非常妙

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100100;

int n;
int b[2 * N], idx;

int main()
{
    scanf ("%d", &n);
    for(int i = 0; i < n; i ++)
    {
        int l, r;
        scanf("%d %d", &l, &r);
        b[idx ++] = l * 2;//标记左端点为偶数。  就算右端点+1，原来左端点比右端点扩大后依然大
        b[idx ++] = r * 2 + 1;// 标记右端点为奇数。  
    }

sort(b, b + idx);

int res = 1, t = 0;
for(int i = 0; i < idx; i ++)
{
    if(b[i] % 2 == 0) t ++;
    else t --;
    res = max(res, t);
}
printf ("%d\n", res);
return 0;
}


纸牌均分

https://www.luogu.com.cn/problem/P1106 删数问题 找到高峰就删

前缀和

例题 https://www.acwing.com/problem/content/description/4963/ 子串简写

一维前缀和 —— 模板题 AcWing 795. 前缀和
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

二维前缀和 —— 模板题 AcWing 796. 子矩阵的和

image-20230821143401897S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

例题 K倍区间 https://www.acwing.com/problem/content/description/1232/

//关键是求序列个数的小技巧和搞懂cnt[0]是一个数本身取余K等于0时也可作为一个答案
#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 100010;
int n,k;
LL A[N];
LL s[N],cnt[N];//cnt计算相同余数的序列的个数总和 
LL res;//计算不相等的余数的个数总和 

int main(){
    scanf("%d %d",&n,&k);

//为什么赋值为1？
//因为我们的思路是找两个序列和a%k和b%k的余数相同的个数
//而我们的前缀和一般是不包含S0这个东西的，因为没有意义，但是这道题有意义
//样例里面前缀和序列%k之后是1 1 0 0 1，两两比较，我们只能找到四个
//为什么少了两个？因为我们不一定需要两个序列，单个序列取余=0也构成K倍区间
//也就是说s3 s4这两个区间是能单独成K倍区间的，而我们的思路是找两个序列比较
//此时，我们就要假设S0=0是有意义的，我们就可以有(s0，s3),(s0,s4)这两个组合
    cnt[0] = 1;
    for(int i = 1; i <= n; i ++){
        scanf("%lld",&A[i]);
        s[i] = s[i - 1] + A[i];
        s[i] = s[i] % k; 
        res += (cnt[s[i]]);
        cnt[s[i]] ++;//记录序列%k不同余数的个数 
        //cnt[s[i]]要在res之后做，因为它是记录总数，如果下面再加回去会重复。 
        /*不能写成
        cnt[s[i]]++;
        res+=(cnt[s[i]]);
        */
        //用笔写字调试一下就知道了 
    }
    //cnt[0] = 1; 
    /*for(int i = 1; i <= n; i ++){
        /*for(int j = i; j <= n; j ++){
            if(s[j] == 0 && j > 0) break;
            if((s[j] - s[i - 1]) % k == 0){
                res ++;
            }
        }
        改成一重循环可以从这里删去。
        这段代码的含义是： 当j固定时，在1-R之间，
                        找到有多少个L，满足([S[右端点] - S[左端点])%k == 0
        从含义上优化代码
        空间换时间 
        */
        //res += (cnt[s[i]]);
    /*我刚开始迷惑为什么不是当cnt[s[i]]>=2的时候才加， 
      现在懂了，因为不一定是两个区间的重叠序列构成K倍区间，
      一个序列本身如果连续和%k=0也构成K倍区间。故所有的都要加上
    */   

    /*10^10>10^8 TLE -> 要改为一重循环*/
    printf("%lld\n",res);
    return 0;
}

作者：Safe_Sound
链接：https://www.acwing.com/solution/content/22093/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

例题 https://www.luogu.com.cn/problem/P3406

差分

一维差分 —— 模板题 AcWing 797. 差分

二维差分 —— 模板题 AcWing 798. 差分矩阵

#include<iostream>
using namespace std;

const int N =1010;

int a[N][N],b[N][N];
int n, m ,q;

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 +1] -= c;
    b[x2 +1][y2+1] +=c;
}


int main()
{
    scanf("%d%d%d", &n, &m, &q);
    

    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);


    

    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            insert(i, j, i, j, a[i][j]);
            
    while( q-- )
    {
        int x1, x2, y1, y2, c;
        cin >> x1 >> y1>> x2 >> y2 >> c;
        insert(x1,y1, x2, y2, c);
    }
    
    //求前缀和
    
    for(int i = 1; i<=n; i++)
        for(int j = 1; j<= m; j++)
        b[i][j] += b[i-1][j] +b[i][j-1] -b[i-1][j-1];
        
    for(int i = 1; i<=n; i++)
    {
        for(int j = 1; j<= m; j++)
        printf("%d ", b[i][j]);
        puts("");
    }
    return 0;

}

位运算(待更)

离散化

如果数据范围小的话（10的五次方以内）用前缀和也可

C++用vector作离散化

下面是去重函数的用法

https://blog.csdn.net/tjcwt2011/article/details/125281748?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169275072116800184115652%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169275072116800184115652&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~baidu_landing_v2~default-1-125281748-null-null.142^v93^chatgptT3_1&utm_term=C%2B%2B%E5%8E%BB%E9%87%8D%E5%87%BD%E6%95%B0&spm=1018.2226.3001.4187

去重完用sort排序最后用二分查找（好像是先排序后去重

二分函数lower_bound（大于等于） upper_bound（大于）

https://blog.csdn.net/weixin_51566349/article/details/128086465?ops_request_misc=&request_id=&biz_id=102&utm_term=lower_bound&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-1-128086465.nonecase&spm=1018.2226.3001.4187

https://www.acwing.com/solution/content/80100/这个代码解释非常详细

csdn的这个博客也很不错(11.11)

https://blog.csdn.net/qq_54773252/article/details/123286277?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169968370116800182120590%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=169968370116800182120590&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~hot_rank-2-123286277-null-null.nonecase&utm_term=%E7%A6%BB%E6%95%A3%E5%8C%96&spm=1018.2226.3001.4450

区间合并

好多端点问题都是贪心

https://www.acwing.com/solution/content/2615/更新维护区间（很重要）

2.第二章 数据结构

链表和邻接表

单链表

用的最多的是邻接表

（存储图和树）

https://www.acwing.com/solution/content/16251/

双链表

添加的顺序不能反

邻接表

栈和队列

表达式求值(中缀 后缀）一般是二元（不包括符号）

单调栈

https://leetcode.cn/problems/maximal-rectangle/solutions/1861698/by-ac_oier-k02i/ 前缀和+单调栈

力扣 84 85 经典

https://www.bilibili.com/video/BV1dY4y1q7tL/?spm_id_from=333.788&vd_source=4452cbcad134fb17ec9cfb03a0acbdac 讲的真好

https://www.acwing.com/problem/content/description/1415/

例题 https://www.luogu.com.cn/problem/P2947

例题 https://leetcode.cn/problems/daily-temperatures/description/

https://www.bilibili.com/video/BV1VN411J7S7/?spm_id_from=333.337.search-card.all.click&vd_source=4452cbcad134fb17ec9cfb03a0acbdac 灵神讲解很好

例题洛谷P2866

#include<bits/stdc++.h>
using namespace std;
stack<int> st;
int n;
int main(){
	cin >> n;
	long long ans= 0; 
	long long cnt = 0;
	for(int i = 1 ; i <=n ; i ++){
		int x;
		cin >> x;	
		while(!st.empty()&&st.top()<=x){
				st.pop();
				cnt--; 
			}
			ans+=cnt;
			st.push(x);
			cnt++;
		}
	}
	cout << ans;
	return 0;
}

优先队列

https://ac.nowcoder.com/acm/contest/78306/E 大顶堆

单调队列

二维单调队列

框架 入 、出、记录答案

https://www.bilibili.com/video/BV1bM411X72E/?spm_id_from=333.337.search-card.all.click&vd_source=4452cbcad134fb17ec9cfb03a0acbdac

https://www.acwing.com/solution/content/97229/这个讲解很好

滑动窗口的框架

1.入

2.出

3.记录答案

题目 https://www.acwing.com/blog/content/29432/

用STL的双端队列deque非常方便

例题 洛谷P2032

#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
struct node{int v,id;}a[N];
deque<node> q;
int n,k;
int main(){
	cin >> n >>k;
	for(int i= 1; i <= n; i ++){
		cin >> a[i].v;
		a[i].id = i;
	}
	for(int i = 1; i <= n; i ++){
		while(!q.empty()&&q.back().v<a[i].v){
			q.pop_back();
		}
		q.push_back(a[i]);
		if(q.front().id==i-k)q.pop_front();
		if(i>=k)cout << q.front().v<<endl;
	}
	return 0;
}

好消息，虽然抽象但是题型固定就那几个

https://www.acwing.com/solution/content/27437/ 这个非常易于适合理解单调栈

单调栈：见博客

单调队列：见博客https://blog.csdn.net/qq_50285142/article/details/120245122?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169761847116800180675961%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169761847116800180675961&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-120245122-null-null.142^v96^pc_search_result_base1&utm_term=%E5%8D%95%E8%B0%83%E9%98%9F%E5%88%97&spm=1018.2226.3001.4187

kmp算法（略）

Trie

题一般字符串字母类型少

算法竞赛里的trie树最多26个或者52个字母

并查集

时间复杂度取决于树的深度

路径压缩使树的深度变小，提高查询效率O(1)

https://www.luogu.com.cn/problem/P1455 01背包+并查集

https://www.cnblogs.com/Eleven-Qian-Shan/p/13154721.html 很好的并查集博客

https://blog.csdn.net/hahalidaxin/article/details/51017473 一个不错的题解

https://www.luogu.com.cn/training/3065#problems 模板题

https://www.cnblogs.com/z-sm/p/12383918.html

https://leetcode.cn/circle/discuss/qmjuMW/

https://www.acwing.com/solution/content/33345/

https://www.acwing.com/activity/content/problem/content/886/ 模板题，记得合并前判断是否已经合并，不然size会加多

https://cloud.tencent.com/developer/article/2068345

https://pintia.cn/problem-sets/994805342720868352/exam/problems/994805354108403712?type=7&page=1

//模板
#include<iostream>

using namespace std;

const int N=100010;
int p[N];//定义多个集合

int find(int x)
{
    if(p[x]!=x) p[x]=find(p[x]);
    /*
    经上述可以发现,每个集合中只有祖宗节点的p[x]值等于他自己,即:
    p[x]=x;
    */
    return p[x];
    //找到了便返回祖宗节点的值
}

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) p[i]=i;
    while(m--)
    {
        char op[2];
        int a,b;
        scanf("%s%d%d",op,&a,&b);
        if(*op=='M') p[find(a)]=find(b);//集合合并操作
        else
        if(find(a)==find(b))
        //如果祖宗节点一样,就输出yes
        printf("Yes\n");
        else
        printf("No\n");
    }
    return 0;
}

https://www.cnblogs.com/zhxmdefj/p/11117791.html 并查集、带权并查集博客

堆

https://www.acwing.com/solution/content/3258/

#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);

priority_queue<int, vector<int>, greater<int>> heap;
while (n -- )
{
    int x;
    scanf("%d", &x);
    heap.push(x);
}

int res = 0;
while (heap.size() > 1)
{
    int a = heap.top(); heap.pop();
    int b = heap.top(); heap.pop();
    res += a + b;
    heap.push(a + b);
}

printf("%d\n", res);
return 0;

}

哈希

https://www.acwing.com/activity/content/problem/content/8034/ 感觉查找匹配还是哈希好写一些

https://www.acwing.com/activity/content/problem/content/8029/ 四平方和

https://www.bilibili.com/video/BV1SZ4y1z7wT/?spm_id_from=333.337.search-card.all.click&vd_source=4452cbcad134fb17ec9cfb03a0acbdac

https://blog.csdn.net/qq_51439643/article/details/122983920?spm=1001.2014.3001.5502 字符串哈希

树状数组

求逆序对 https://www.luogu.com.cn/problem/P1908

https://www.bilibili.com/video/BV1ce411u7qP/?spm_id_from=333.337.search-card.all.click&vd_source=4452cbcad134fb17ec9cfb03a0acbdac

https://www.bilibili.com/video/BV14r421W7oR/?spm_id_from=333.337.search-card.all.click&vd_source=4452cbcad134fb17ec9cfb03a0acbdac 原理讲得好 根据二进制位从右往左拆分

查询 更新 都是 O（logN）

例题 动态求区间和
树状数组 模板1
#include<bits/stdc++.h>

using namespace std;

const int N=100009;

int a[N],tr[N];

int n,m;

//每个数的间隔，背下来就行
int lowbit(int x)
{
    return x&-x;
}

//第x个数加上v
int add(int x,int v)
{
    //因为树状数组的性质，加一个数，只影响logn个数，所有不用全加完
    //从当前位置开始加，每个间隔是lowbit(i)，一直加到最后
    for(int i=x;i<=n;i+=lowbit(i))
        tr[i]+=v;
}

//返回x的前缀和
int qurry(int x)
{
    //因为树状数组的性质，求前缀和，只用加logn个数，所有不用全加完
    //从当前位置开始累加，每个间隔是lowbit(i)，一直加到i==0停止
    int cnt=0;
    for(int i=x;i!=0;i-=lowbit(i)){
        cnt+=tr[i];
    }
    return cnt;

}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
        add(i,a[i]);//第i个数加上a[i]

while(m--)
{
    int k,x,y;
    scanf("%d%d%d",&k,&x,&y);
    if(k==0) printf("%d\n",qurry(y)-qurry(x-1));
    else add(x,y);
}
return 0;

}

树状数组 模板2

https://www.luogu.com.cn/article/g7ci886q

区间修改、区间查询：

https://blog.csdn.net/Wu_while/article/details/119491559

[同时支持区间修改、区间查询](

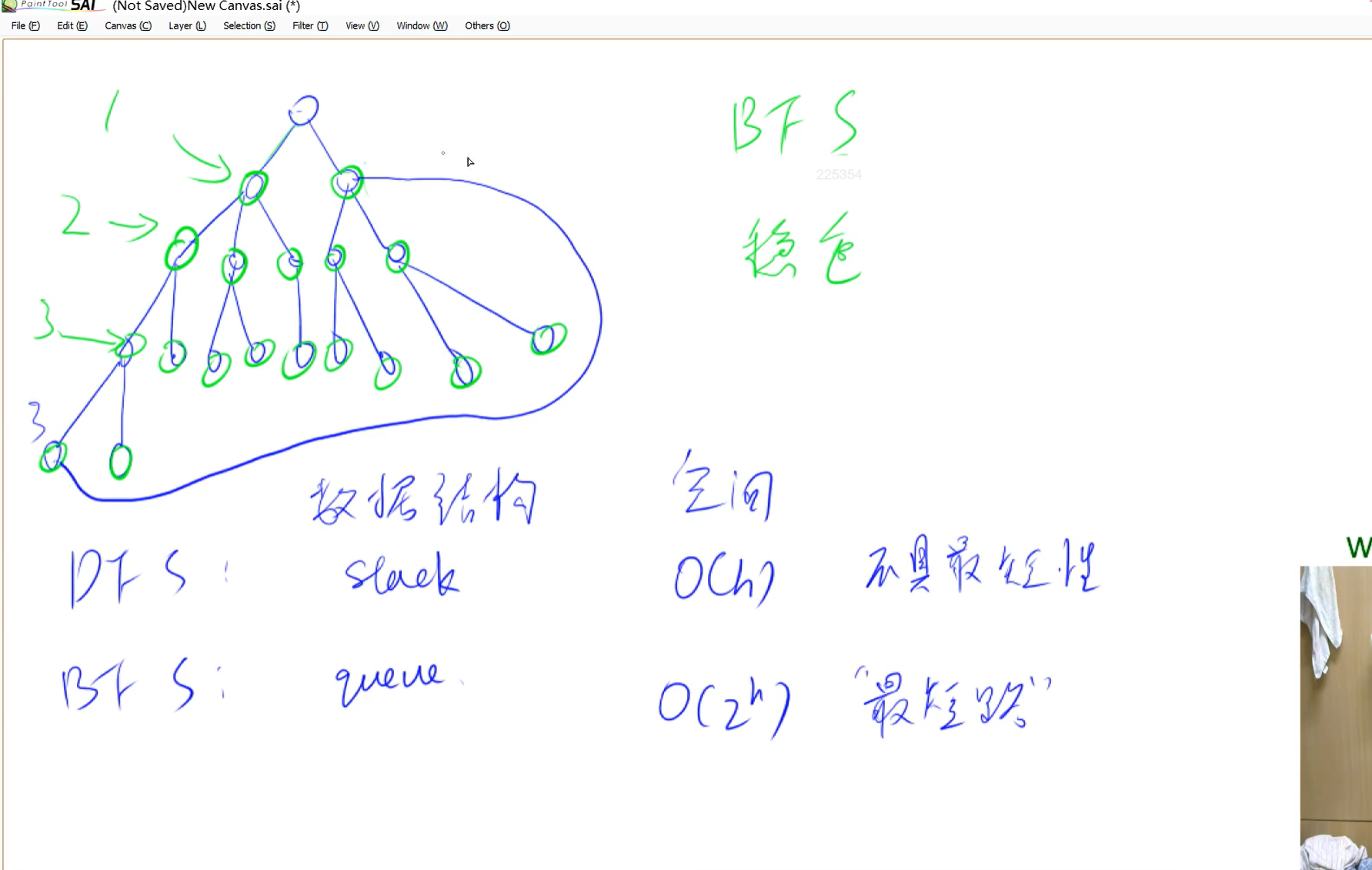
3.第三章 搜索与图论

DFS和BFS区别

https://leetcode.cn/problems/binary-tree-level-order-traversal/solutions/244853/bfs-de-shi-yong-chang-jing-zong-jie-ceng-xu-bian-l/

递归

https://www.bilibili.com/video/BV1UD4y1Y769/?spm_id_from=333.880.my_history.page.click&vd_source=4452cbcad134fb17ec9cfb03a0acbdac

https://leetcode.cn/problems/maximum-depth-of-binary-tree/solutions/2010612/kan-wan-zhe-ge-shi-pin-rang-ni-dui-di-gu-44uz/ 二叉树最大深度

https://leetcode.cn/problems/minimum-depth-of-binary-tree/submissions/511924007/ 二叉树最小深度，要考虑全面 （好题）

https://leetcode.cn/problems/path-sum/description/ 路径总和I (AC)

https://leetcode.cn/problems/path-sum-ii/description/ 路径总和II (AC)

https://leetcode.cn/problems/sum-root-to-leaf-numbers/ 求根节点到叶节点之和(AC)

https://leetcode.cn/problems/binary-tree-paths/description/ 好题 二叉树的所有路径

https://leetcode.cn/problems/vertical-order-traversal-of-a-binary-tree/ 二叉树垂序遍历（未做）

https://leetcode.cn/problems/same-tree/ 相同的树

https://leetcode.cn/problems/symmetric-tree/ 对称二叉树

https://leetcode.cn/problems/balanced-binary-tree/solutions/2015068/ru-he-ling-huo-yun-yong-di-gui-lai-kan-s-c3wj/ 平衡二叉树

https://leetcode.cn/problems/binary-tree-right-side-view/solutions/2015061/ru-he-ling-huo-yun-yong-di-gui-lai-kan-s-r1nc/ 二叉树的右视图

https://leetcode.cn/problems/binary-tree-right-side-view/ 二叉树的右视图， BFS DFS都可以用

https://leetcode.cn/problems/invert-binary-tree/solutions/791028/yi-pian-wen-zhang-dai-ni-chi-tou-dui-che-21l9/ 对称性递归

https://leetcode.cn/problems/invert-binary-tree/solutions/73159/dong-hua-yan-shi-liang-chong-shi-xian-226-fan-zhua/ 好题 后序遍历

节点与其祖先之间的最大差值 好题

换个角度看问题：对于一条从根出发向下的路径，我们要计算的实际上是这条路径上任意两点的最大差值。

递归到叶子时，mx\textit{mx}mx 是从根到叶子的路径上的最大值，mn\textit{mn}mn 是从根到叶子的路径上的最小值，所以 mx−mn\textit{mx}-\textit{mn}mx−mn 就是从根到叶子的路径上任意两点的最大差值。

所以无需每个节点都去更新答案，而是在递归到终点时才去更新答案。

作者：灵茶山艾府
链接：https://leetcode.cn/problems/maximum-difference-between-node-and-ancestor/solutions/2232367/liang-chong-fang-fa-zi-ding-xiang-xia-zi-wj9v/

根到叶路径上的不足节点

https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/solutions/2277376/python3-di-gui-xiang-jie-1080-gen-dao-xi-cc4a/

https://leetcode.cn/problems/validate-binary-search-tree/ 验证二叉搜索树

https://leetcode.cn/problems/search-in-a-binary-search-tree/description/ 二叉搜索树中的搜索

https://leetcode.cn/problems/range-sum-of-bst/description/ 二叉搜索树的范围和

https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/submissions/512285467/ gpt生成的该题题解

删点成林 https://leetcode.cn/problems/delete-nodes-and-return-forest/ 未做

二叉树中的最长交错路径 https://leetcode.cn/problems/longest-zigzag-path-in-a-binary-tree/ 未做

https://leetcode.cn/problems/diameter-of-binary-tree/solutions/2227017/shi-pin-che-di-zhang-wo-zhi-jing-dpcong-taqma/ 树形DP

二叉树的直径 https://leetcode.cn/problems/diameter-of-binary-tree/solution/shi-pin-che-di-zhang-wo-zhi-jing-dpcong-taqma/

二叉树中的最大路径和 https://leetcode.cn/problems/binary-tree-maximum-path-sum/solution/shi-pin-che-di-zhang-wo-zhi-jing-dpcong-n9s91/ （反复调试AC，灵神题解很优美）

https://www.acwing.com/activity/content/problem/content/9764/ 蓝桥杯 大臣的旅费 树的直径，树形DP

https://www.acwing.com/activity/content/problem/content/9767/ 木棒 每日一题

https://www.acwing.com/activity/content/problem/content/9769/ 糖果

回溯

https://www.luogu.com.cn/problem/P8642 洛谷绿题

子集

https://www.bilibili.com/video/BV1mG4y1A7Gu/?spm_id_from=333.880.my_history.page.click&vd_source=4452cbcad134fb17ec9cfb03a0acbdac

https://leetcode.cn/problems/palindrome-partitioning/description/ 分割回文串（灵神代码优美）

https://leetcode.cn/problems/letter-case-permutation/ 字母大小写全排列

组合

https://www.bilibili.com/video/BV1xG4y1F7nC/?spm_id_from=333.788&vd_source=4452cbcad134fb17ec9cfb03a0acbdac

https://leetcode.cn/problems/combination-sum-iii/description/ 组合总和III

https://leetcode.cn/problems/generate-parentheses/ 括号生成

https://ac.nowcoder.com/acm/contest/76133/E 牛客周赛例题

情况1:两个点最短路相同，连一起最短路仍然不变，可以加边

情况2:两个最短路的绝对值差为1

无解的情况

1、[0,1,2,4,4,5,6]：没有3

2、m<n-1 点<边的数量

第一次构造 第一种情况

第二次构造 第二种情况

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n, m;
const int mod = 1e9 + 7;
signed main(){
	cin >> n >> m;
	//第二种情况 
	if(m < n - 1){
		cout << -1 << endl;
		return 0;
	}
	//存层次相同的点 
	vector<int> g[n + 10];
	vector<int> a(n + 1);
	int ma = -1;
	for(int i = 1; i <= n; i ++){
		cin >> a[i];
		ma = max(ma, a[i]);
		g[a[i]].push_back(i);
	}
	vector<pair<int, int>> ans;
	//第一种情况 
	for(int i = 1; i  <= ma; i ++){
		if(g[i - 1].empty()){
			cout << "-1";
			return 0;
		}
	}
	for(int i = 1; i <= ma; i ++){
		for(auto k: g[i]){
			ans.push_back({g[i - 1][0], k});
		}
	}
	//第一种情况，相同层次连边 
	for(int i = 1; i <= ma; i ++){
		for(int j = 1; j < g[i].size(); j ++){
			for(int k = j - 1; k >= 0; k --){
				ans.push_back({g[i][j], g[i][k]});
				if(ans.size() == m)break;
			}
			if(ans.size() == m) break;
		}
		if(ans.size() == m) break;
	}
	//第二种，每个层次与上一层次的除了第一个点连接 
	for(int i = 1; i <= ma; i ++){
		for(int j = 1; j < g[i - 1].size(); j ++){
			for(int k = 1; k < g[i].size(); k ++){
				ans.push_back({g[i - 1][j],g[i][k]});
				if(ans.size()==m)break;
			}
			if(ans.size() == m)break;
		}
		if(ans.size() == m)break;
	} 
	if(ans.size() < m){
		cout << -1;
	}else{
		for(auto i : ans){
			cout<<i.first <<" "<<i.second << endl;
		}
	}
	return 0;
}

image-20230825090148050

深度优先搜索(DFS)

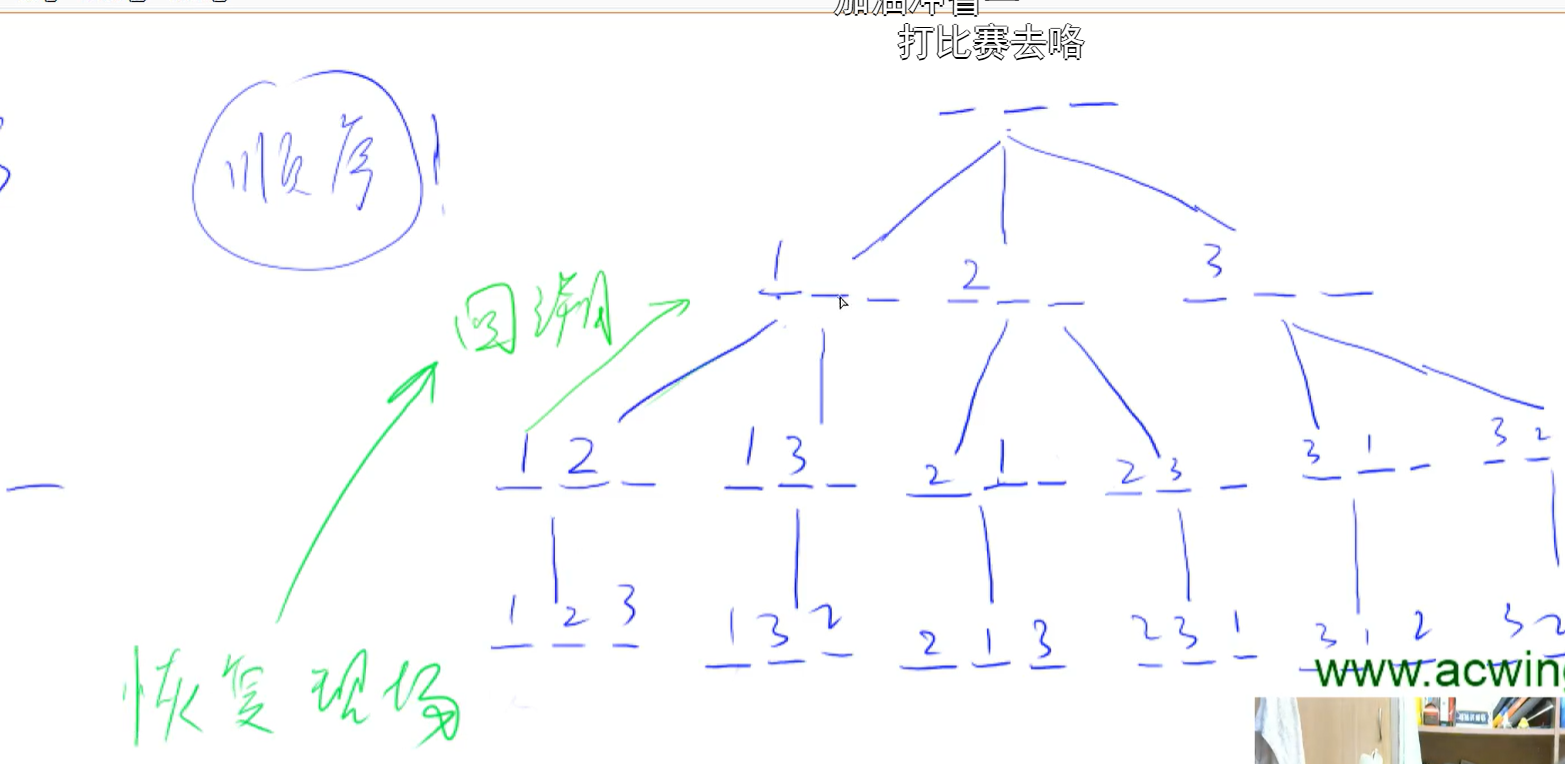
两个很重要的概念：回溯 剪枝

每个DFS都一定对应一个搜索树

https://www.acwing.com/solution/content/30988/

https://www.luogu.com.cn/problem/solution/P5194 求最大值 从后往前

https://www.cnblogs.com/lcez56jsy/p/10705834.html 迷宫 求方案数

https://www.luogu.com.cn/problem/P1101 单词方阵（搜一个字符串）

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;

const int maxn = 110;
const int dx[] = {1, 1, 1, 0, 0, -1,-1,-1 };  //方向数组 
const int dy[] = {1, 0,-1, 1,-1, 0 , 1,-1 };
const string cmp = "yizhong"; // 比较数组 

char A[maxn][maxn], ans[maxn][maxn];
int mark[maxn][maxn], n;

void dfs(int x,int y) {
	for(int i = 0;i < 8;i++) {  //枚举8个方向 
		int flag = 1;
		for(int j = 1;j <= 6;j++) { //以1个方向比较 “izhong”   
			int nx = x + j*dx[i];    
			int ny = y + j*dy[i];
			if(nx < 1 || nx > n || ny < 1 || ny > n) { //判越界 
				flag = 0;
				break;
			}
			if(cmp[j] != A[nx][ny]) {  //判断第j位是否符合 
				flag = 0;
				break;
			}
		}
		if(flag == 0) continue;
		for(int j = 0;j <= 6;j++) { //符合就记录在ans数组里 
			int nx = x + j*dx[i];
			int ny = y + j*dy[i];
			ans[nx][ny] = A[nx][ny];
		}
	}
	return;
}

int main() {
	cin >> n;
	for(int i = 1;i <= n;i++) {
		for(int j = 1;j <= n;j++) {
			cin >> A[i][j];
		}
	}
	
	for(int i = 1;i <= n;i++) { 
		for(int j = 1;j <= n;j++) {
			if(A[i][j] == 'y') dfs(i,j);//如果发现有y就开始搜索 
		}
	}
	for(int i = 1;i <= n;i++) { //输出 
		for(int j = 1;j <= n;j++) {
			if(ans[i][j] == 0) ans[i][j] = '*';//如果没有改动就输出* 
			cout << ans[i][j];
		}
		cout << endl;
	}
	return 0;
}

https://www.luogu.com.cn/problem/P1019 单词接龙https://www.cnblogs.com/dx123/p/17486562.html

最后ans - 1是因为有前面的*，前面加 * 可以方便j从1开始枚举，不用特判

经典题目 八皇后

广度优先搜索(BFS)

迷宫问题 https://cloud.tencent.com/developer/article/1176807把DFS和BFS区别讲的很明白

2019蓝桥 https://blog.csdn.net/m0_56312312/article/details/123671856 思路很好，字典序数组按照顺序排好了，第一个得到的路径必然是最短的并且字典序最小的

https://www.luogu.com.cn/paste/sa0zary9 题单

例题蓝桥国赛 迷宫与陷阱 ：https://www.luogu.com.cn/problem/P8673

例题 全球变暖 https://www.acwing.com/problem/content/description/1235/

注意 迷宫（这题不建议用bfs） https://www.cnblogs.com/lcez56jsy/p/10705834.html 和DFS的区别（回溯）

Flood fill(洪水灌溉)

1.多少个连通块

不是所有最短路都用BFS，只能当边权都是1时，一般情况都是用最短路算法

BFS函数里一般都用队列

2.多少个被淹没

代码

#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e3 + 10;
int n;
char g[N][N];
bool vis[N][N];
int judge[N][N];
int cnt;
queue<PII> q;
int dx[5] = {0,0,1,0,-1},dy[5] = {0,1,0,-1,0};
void BFS1(int x,int y){
    while(!q.empty()){
        auto t = q.front();
        q.pop();
        for(int i = 0; i < 5;i  ++){
            int x = dx[i] + t.first, y = dy[i] +t.second;
            if(x>=1&&x<=n&&y>=1&&y<=n&&vis[x][y]==false&&g[x][y]=='#'&&(g[x-1][y]=='.'||g[x+1][y]=='.'||g[x][y-1]=='.'||g[x][y+1]=='.')){
                vis[x][y] = true;
                judge[x][y]= 1; 
                q.push({x,y});
            }
        }
    }
}
void BFS2(int x,int y){
    int flag = 0;
    while(!q.empty()){
        auto t = q.front();
        q.pop();
        
        for(int i = 0; i < 5; i ++){
            int x=  dx[i] +t.first,y=dy[i]+t.second;
            if(x>=1&&x<=n&&y>=1&&y<=n&&g[x][y]=='#'&&vis[x][y]==false){
                vis[x][y] = true;
                if(judge[x][y]==0){
                    flag = 1;
                }
                q.push({x,y});               
            }
        }
    }
    if(flag == 0)cnt++;
}
int main(){
    cin >> n;
    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= n; j ++){
            cin >> g[i][j];
        }
    }
      for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= n; j ++){
            if(g[i][j] == '#'&&vis[i][j]==false){
                q.push({i,j});
                BFS1(i,j);
            }
        }
    }  
    memset(vis,false,sizeof vis);
    for(int i = 1; i <= n; i ++){
        for(int j  = 1; j <= n; j ++){
            if(g[i][j] == '#'&&vis[i][j]==false){
                q.push({i,j});
                    BFS2(i,j);
            }
        }
    }
    cout << cnt;
    return 0;
}

岛屿个数 https://www.acwing.com/problem/content/description/4962/

两个BFS，特别好的题，注意海水渗透要8个方向。

#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 55;
int T;
char g[N][N];
queue<PII> q;
int n,m;
int dx[8] = {1,0,-1,0, 1, 1 ,-1, - 1};
int dy[8] = {0,1,0,-1,-1,1,-1,1};
void BFS1(){
    q.push({0,0});
    g[0][0] = '2';
    while(!q.empty()){
        auto t = q.front();
        q.pop();
        for(int i = 0 ;i  < 8; i ++){
            int x = t.first + dx[i], y = t.second + dy[i];
            if(x >= 0 && x<=n+1 && y >=0 && y <=m + 1 && g[x][y]=='0'){
                g[x][y] = '2';
                q.push({x,y});
            }
        }
    }
}
void BFS2(int x, int y){
    q.push({x,y});
    g[x][y] = '2';
    while(!q.empty()){
        auto t = q.front();
        q.pop();
        for(int i = 0; i < 4; i ++){
            int x = t.first + dx[i], y = t.second + dy[i];
            if(x >= 1 && x <= n && y>=1&&y <=m && (g[x][y]=='0'||g[x][y]=='1')){
                g[x][y] = '2';
                q.push({x,y});
            }
        }
    }
}
int main(){
    cin >> T;
    // int ans = 0;
    while(T --){
        memset(g,'0',sizeof g);
        cin >> n >> m;
             int ans = 0;
        for(int i = 1; i <= n; i ++){
            for(int j = 1; j <= m; j ++){
                cin >> g[i][j];
            }
        }
        BFS1();
        //能形成岛屿，里面肯定不会进海水
        for(int i = 1; i <= n; i ++){
            for(int j =1; j <= m; j ++){
                if(g[i][j] == '1'){
                    BFS2(i, j);
                    // cout <<"i = =" << i <<"j == " << j << endl;
                    ans ++;
                    
                }
            }
        }
        cout << ans << endl;
    }

}

树与图的存储（10.21）

https://www.bilibili.com/video/BV1mJ411S7BB/?spm_id_from=333.337.search-card.all.click&vd_source=4452cbcad134fb17ec9cfb03a0acbdac

这个链式前向星讲的特别好↑

树是特殊的图，所以只讲图就行

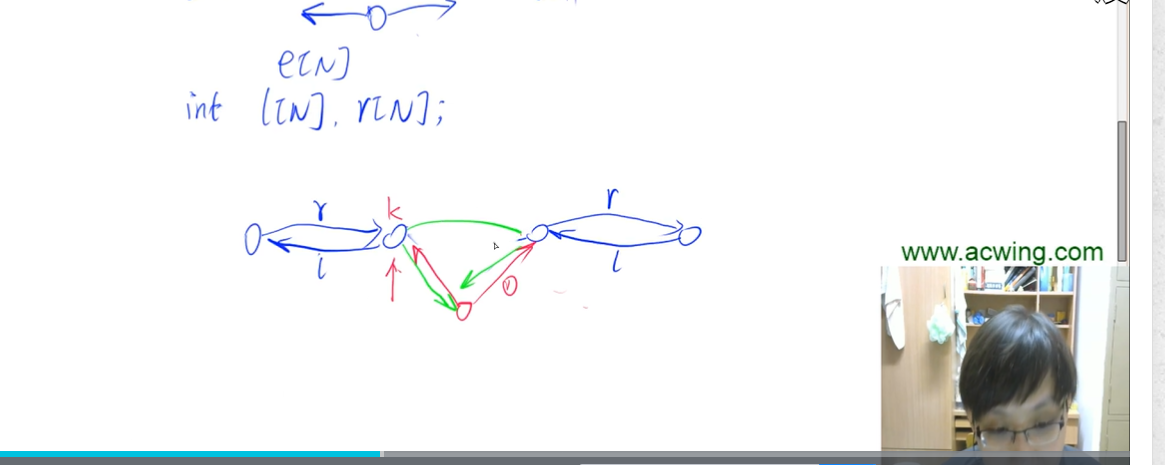
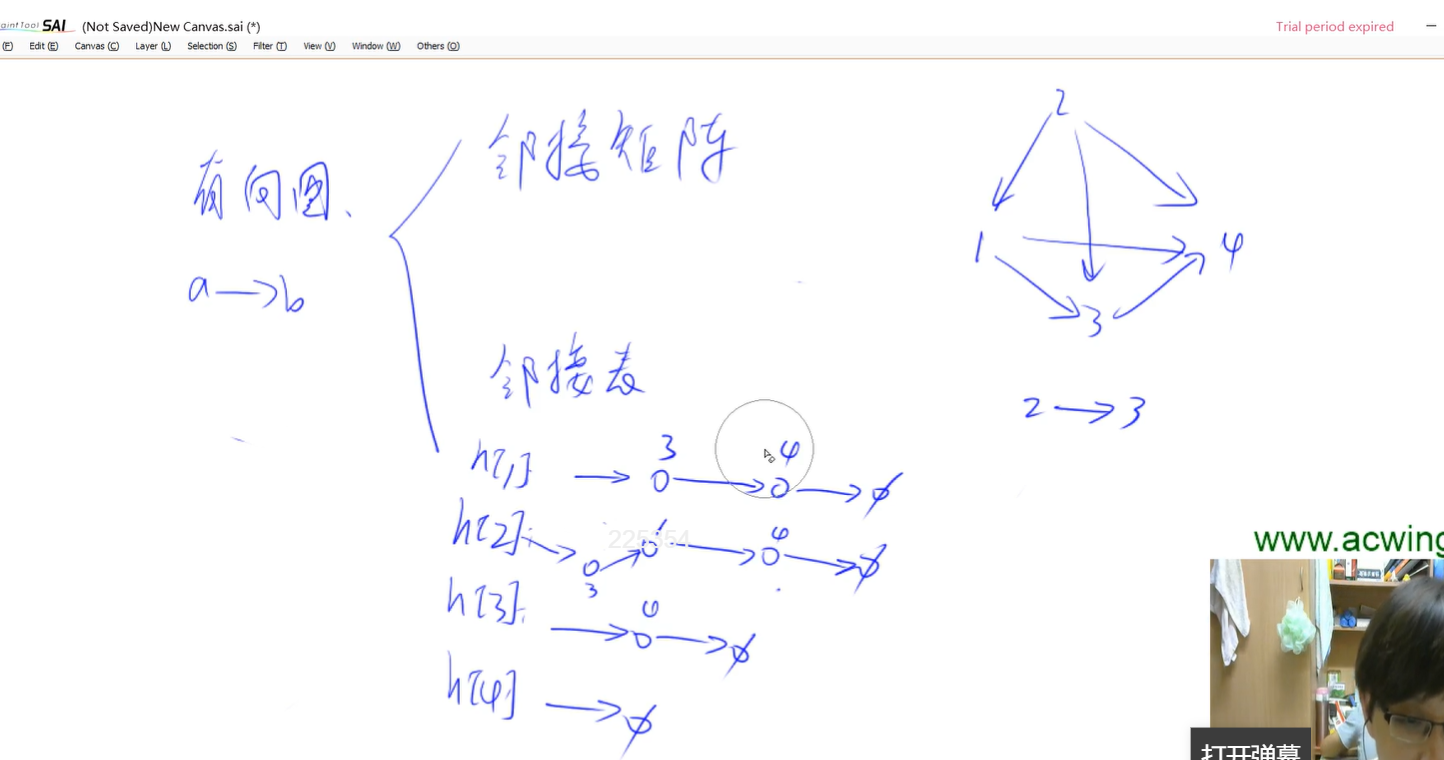
图：有向图，无向图，边有无方向，无向图可以看作特殊的有向图，所以只要看有向图

有向图（a->b)：

邻接矩阵g[a] [b] a->b,有重边保留一条就可以了

邻接表

树与图的深度优先遍历

image-20231204141022311

**https://leetcode.cn/circle/discuss/FyPTTM/**宝藏

讲解了为什么要反向建边 https://www.163.com/dy/article/E01JK0430538071X.html

https://www.luogu.com.cn/problem/P3916

洛谷这个题↑正向遍历超时了 n 1e5 ，用反向遍历更适合

思路真妙，把大的先走完，打上标记，肯定就是最大的了

图的讲解(2023.12.4很好) https://www.luogu.com.cn/problem/solution/P5318

这个邻接表写法nice↓

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;

const int MAXN = 100010;

std::vector<int> G[MAXN];
int n, m;
bool visited[MAXN];
queue<int> q;

void dfs(int x, int cur) {//x指当前所在的节点，cur指已遍历过的节点个数
	visited[x] = true;//标记以避免重复访问
	cout << x << " ";//输出
	if (cur == n) return ;
	for (int i=0; i<G[x].size(); i++)
		if (!visited[G[x][i]]) dfs(G[x][i], cur+1);//记得要判断是否遍历过
}

void bfs(int x) {
	memset(visited, false, sizeof(visited));//记得一定要清空
	visited[x] = true;
	q.push(x);
	while (!q.empty()) {
		int v = q.front();
		q.pop();//记得要弹出，否则会一直在第一层遍历
		cout << v << " ";//输出
		for (int i=0; i<G[v].size(); i++) 
			if (!visited[G[v][i]]) {
				visited[G[v][i]] = true;
				q.push(G[v][i]);//记得要入队
			}
	}
}

int main() {
	cin >> n >> m;
	for (int i=1; i<=m; i++) {
		int u, v;
		cin >> u >> v;
		G[u].push_back(v);//标准邻接表建有向图
	}
	for (int i=1; i<=n; i++) sort(G[i].begin(), G[i].end());//标准vector排序
	dfs(1, 0);
	cout << endl;
	bfs(1);
	cout << endl;
	return 0;//完结撒花！
}

非常重要!!!由前+中/后+中构建序列 模板（字符串切割 + 练习STL substr）

https://www.luogu.com.cn/problem/solution/P1827 

由中序和前序求后序
#include<bits/stdc++.h>
using namespace std;
string pre,inor;
void dfs(string pre,string inor){
    if(pre.empty())return;
    char root = pre[0];
    int k = inor.find(root);
    pre.erase(pre.begin());
    string leftpre = pre.substr(0,k);
    string rightpre = pre.substr(k);
    string leftinor = inor.substr(0,k);
    string rightinor = inor.substr(k + 1);
    dfs(leftpre,leftinor);
    dfs(rightpre,rightinor);
    printf("%c",root);

}
int main(){
    cin >> inor >>pre ;
    dfs(pre,inor);
    putchar('\n');
    return 0;
}

https://www.luogu.com.cn/problem/P1030

由中序和后序求前序
#include<bits/stdc++.h>
using namespace std;
string inor,post;
void solve(string inor,string post){
    if(post.empty())return;
    char root = post[post.size() - 1];
    post.erase(post.end()-1);
    int k = inor.find(root);
    
    string inorleft = inor.substr(0,k);
    string inorright= inor.substr(k + 1);
    string postleft = post.substr(0,k);
    string postright = post.substr(k);
    cout << root;
    solve(inorleft,postleft);
    solve(inorright,postright);

}
int main(){
    cin >> inor >> post;
    solve(inor,post);
    return 0;
}
#include<string>
#include<cstring>
#include<iostream>
#include<cstdio>
using namespace std;
string pre,inor;
void work(string pre,string inor)
{
    if(pre.empty())return;
    //如果序列空了，就没必要继续了
    char root=pre[0];
    //取到前序序列的首字母，即根节点
    int k=inor.find(root);
    //找到中序序列中根节点的位置
    pre.erase(pre.begin());
    //删去前序序列中的根节点
    string leftpre=pre.substr(0,k);
    //从0开始切割k个
    string rightpre=pre.substr(k);
    //从k开始切割到最后
    string leftinor=inor.substr(0,k);
    //从0开始切割k个
    string rightinor=inor.substr(k+1);
    //从k+1开始切割到最后
    work(leftpre,leftinor);
    work(rightpre,rightinor);
    printf("%c",root);
    //因为要输出后序序列，所以是左右根
    //先遍历左子树，再右子树，再根节点
}
int main()
{
    cin>>inor>>pre;
    work(pre,inor);
    putchar('\n');
    return 0;
}

树与图的宽度优先遍历(待更)

DAG() 与 拓扑排序（12.4）

知乎的讲解，很好↓[知识点]

https://zhuanlan.zhihu.com/p/135094687

拓扑排序邻接表版[代码]

https://www.acwing.com/problem/content/850/

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
vector<int> G[N];//邻接表 
queue<int> q;//队列操作 
int d[N];//统计入度 
int n,m,cnt,ans[N];//ans数组记录答案 
int main(){
	cin >> n >> m;
	for(int i = 1 ;i <= m; i ++){
		int x,y;
		cin >> x>> y;
		G[x].push_back(y);
		d[y]++;//统计入度 
	}
	for(int i =1; i <= n; i ++){
		if(d[i]==0)q.push(i);//1
	}
	while(q.size()){
		int t = q.front();
		q.pop();
		ans[cnt++] = t;
		for(int i = 0 ; i < G[t].size();i  ++){
			d[G[t][i]]--;//删边操作 
			if(d[G[t][i]]==0) q.push(G[t][i]);//删完后入度为0的话，放入队列 
		}
	}
	if(cnt == n)for(int i = 0; i <cnt; i ++)cout << ans[i]<<" ";
	else cout <<-1;
	return 0;
}

例题

我发现下面两道需要拓扑的题，只需要把一些求ans的代码放到模板里，模板还是不变的

1 .洛谷P1113 杂务

/**
	每个任务前的耗时最长的任务相加即为答案，详情看洛谷深入浅出
**/
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

const int N = 500005;

int ind[N], f[N], a[N];  // ind--入度   f--答案   a--时间
vector<int> edge[N];
queue<int> q;

int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        cin >> a[i];
        while (true) {
            int y;
            cin >> y;
            if (y == 0)
                break;
            edge[y].push_back(x);
            ind[x]++;
        }
    }
    // 步骤一
    for (int i = 1; i <= n; i++) {
        if (ind[i] == 0) {
            q.push(i);
            f[i] = a[i];
        }
    };
    while (!q.empty()) {
        int rhs = q.front();
        q.pop();
        // 步骤二
        for (int i = 0; i < edge[rhs].size(); i++) {
            int u = edge[rhs][i];
            ind[u]--;
            if (ind[u] == 0)
                q.push(u);  // 步骤三
            f[u] = max(f[u], f[rhs] + a[u]);
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        ans = max(ans, f[i]);   // 统计答案
    }
    cout << ans << endl;
    return 0;
}

2.P4017 最大食物链计数

/**
	先找出所有入度为0的，初始链数为1，后面搜到的每个点，都等于各个点链数之和，详情看洛谷深入浅出
**/
#include<bits/stdc++.h>
using namespace std;
const int N = 5e3 + 10;
int ans[N],outd[N],ind[N];
vector<int>G[N];
queue<int>q;
int main(){
    int n,m;
    cin >> n >> m;
    for(int i = 0; i < m; i ++){
        int x,y;
        cin >> x >> y;
        ind[y]++;
        outd[x]++;
        G[x].push_back(y);
    }
    for(int i = 1; i <= n; i ++){
        if(ind[i]==0){
            q.push(i);  
			ans[i] = 1; 
        }

}
while(q.size()){
    auto t = q.front();
    q.pop();
    for(int i = 0 ; i < G[t].size(); i ++){
        int x = G[t][i];
        ind[x] --;
		if(ind[x]==0){
            q.push(x);
        }
        ans[x] = (ans[x] + ans[t])%80112002;
    }
}
int res = 0;
for(int i = 1; i <= n; i ++){
    if(outd[i]==0){
        res= (res + ans[i])%80112002;
    }
}
cout << res;
return 0;

}

最短路径

力扣总结精华

https://leetcode.cn/circle/discuss/FyPTTM/#%E6%9C%80%E7%9F%AD%E8%B7%AF%E5%BE%84

有权单源最短路

无权单源最短路

带权全源最短路

如果是无权单源，可以BFS+队列，有权就不行了

带权单源最短路
Dijkstra

视频演示：

https://www.bilibili.com/video/BV1zz4y1m7Nq/?spm_id_from=333.788.recommend_more_video.0&vd_source=4452cbcad134fb17ec9cfb03a0acbdac

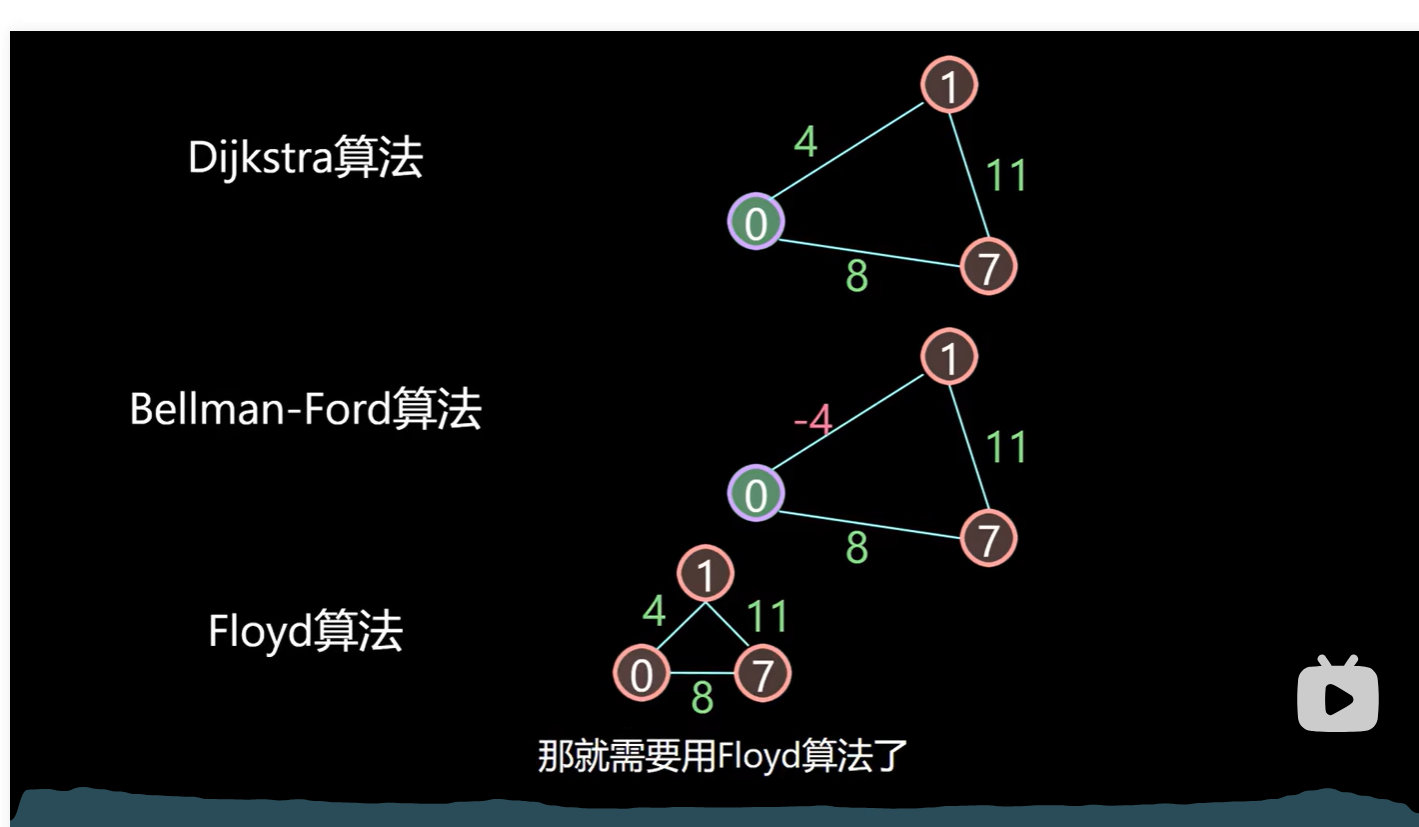
各个算法用途比较

https://www.acwing.com/solution/content/5806/ 代码详解

朴素版
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N=510;

int g[N][N];    //为稠密阵所以用邻接矩阵存储
int dist[N];    //用于记录每一个点距离第一个点的距离
bool st[N];     //用于记录该点的最短距离是否已经确定

int n,m;

int Dijkstra()
{
    memset(dist, 0x3f,sizeof dist);     //初始化距离  0x3f代表无限大

dist[1]=0;  //第一个点到自身的距离为0

for(int i=0;i<n;i++)      //有n个点所以要进行n次 迭代
{
    int t=-1;       //t存储当前访问的点

    for(int j=1;j<=n;j++)   //这里的j代表的是从1号点开始
        if(!st[j]&&(t==-1||dist[j]<dist[t]))     
            t=j;

    st[t]=true;   

    for(int j=1;j<=n;j++)           //依次更新每个点所到相邻的点路径值
        dist[j]=min(dist[j],dist[t]+g[t][j]);
}

if(dist[n]==0x3f3f3f3f) return -1;  //如果第n个点路径为无穷大即不存在最低路径
return dist[n];

}
int main()
{
    cin>>n>>m;

memset(g,0x3f,sizeof g);    //初始化图 因为是求最短路径
                            //所以每个点初始为无限大

while(m--)
{
    int x,y,z;
    cin>>x>>y>>z;
    g[x][y]=min(g[x][y],z);     //如果发生重边的情况则保留最短的一条边
}

cout<<Dijkstra()<<endl;
return 0;

}

对于「稠密图」，应当使用「朴素版」，对于「稀疏图」，应当使用「优先队列版」

堆优化版

（vector邻接表，但是大多用的还是数组模拟邻接表）

/**
	邻接表存的话不用考虑重边，dij算法会取最小的
**/
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
const int N = 1e5 + 10;
// 稀疏图用邻接表来存
vector<PII>G[N];
int dist[N];
bool st[N];
int n,m;
int dijkstra(){
	memset(dist,0x3f,sizeof dist);
	dist[1] = 0;
	// 这里heap中为什么要存pair呢，首先小根堆是根据距离来排的，所以有一个变量要是距离，
    // 其次在从堆中拿出来的时候要知道知道这个点是哪个点，不然怎么更新邻接点呢？所以第二个变量要存点。
    // 这个顺序不能倒，pair排序时是先根据first，再根据second，
     // 这里显然要根据距离排序,对pair排序默认先对first,所以first放距离更省事 
    priority_queue<PII,vector<PII>,greater<PII>>heap;
	heap.push({0,1});
	while(heap.size()){
		auto t = heap.top();
		heap.pop();
		int distance = t.first,node = t.second;
		if(st[node])continue;
		st[node] = true;
	
		for(int i = 0; i < G[node].size(); i ++){
			int newNode = G[node][i].first;
			int len = G[node][i].second;
			if(dist[newNode]>dist[node] + len){
				dist[newNode] = dist[node] + len;
				heap.push({dist[newNode],newNode});
			}
		}
	}
	if(dist[n] == 0x3f3f3f3f)return -1;
	else return dist[n];
}
int main(){
	cin >> n >> m;
	G.resize(n + 1);
	for(int i = 0; i < m; i ++){
		int x,y,z;
		cin >> x >> y >> z;
		G[x].push_back({y,z});
	}
	cout << dijkstra();
	return 0;
}
最短路径 和 各种第二标量

例题PTA甲级 紧急事件

#include<bits/stdc++.h>
using namespace std;
int G[510][510];
int dist[510];
int num[510];//救援队
int n,m,c1,c2;
bool vis[510];
int weight[510];
int num2[510];//最短路数量
void dijkstra(){
    memset(dist,0x3f,sizeof dist);
    dist[c1] = 0;
    num2[c1] = 1;
    num[c1] = weight[c1];
    for(int i = 0; i < n ; i ++){
        int t = -1;
        for(int j = 0; j < n; j ++){
            if(vis[j]==false&&(t==-1||dist[t] >dist[j])){
                t = j;
            }
        }
        vis[t] = true;
        for(int j = 0; j < n; j ++){
            // dist[j] = min(dist[j],dist[t] + G[t][j]);
            if(dist[t] + G[t][j] < dist[j]){
                dist[j] = dist[t] + G[t][j];
                num[j] = num[t] + weight[j];
                num2[j] = num2[t];
                

        }else if(dist[t] +G[t][j] == dist[j]){
            num2[j] += num2[t];
            if(weight[j] + num[t] > num[j])
            num[j] = num[t] + weight[j];
                
                

        }
    }
}
cout << num2[c2] <<" "<<num[c2];

}
int main(){
    cin >>n >> m >>c1>>c2;
    for(int i = 0; i < n; i ++){
        cin >> weight[i];
    }
    memset(G,0x3f,sizeof G);
    while(m --){
        int x,y,z;
        cin >> x >> y >> z;
        G[x][y] = min(G[x][y],z);
        G[y][x] = min(G[y][x],z);
        // G[x][y] = G[y][x]= z;
    }
    dijkstra();
    return 0;
}

书P375

打印路径
void DFS(int s,int v){ //s是起点编号，v是当前访问的顶点编号(从终点开始递归)
	if(v == s){
        printf("%d\n",s);
        return ;
    }
    DFS(s,pre[v]);
    printf("%d\n",v);
}

为什么无法处理负边

https://www.acwing.com/solution/content/6320/详解很好

bellman-ford

与spfa比可能唯一的好处：如果是有边数限制的话，就不能用spfa了

时间复杂度 N*M

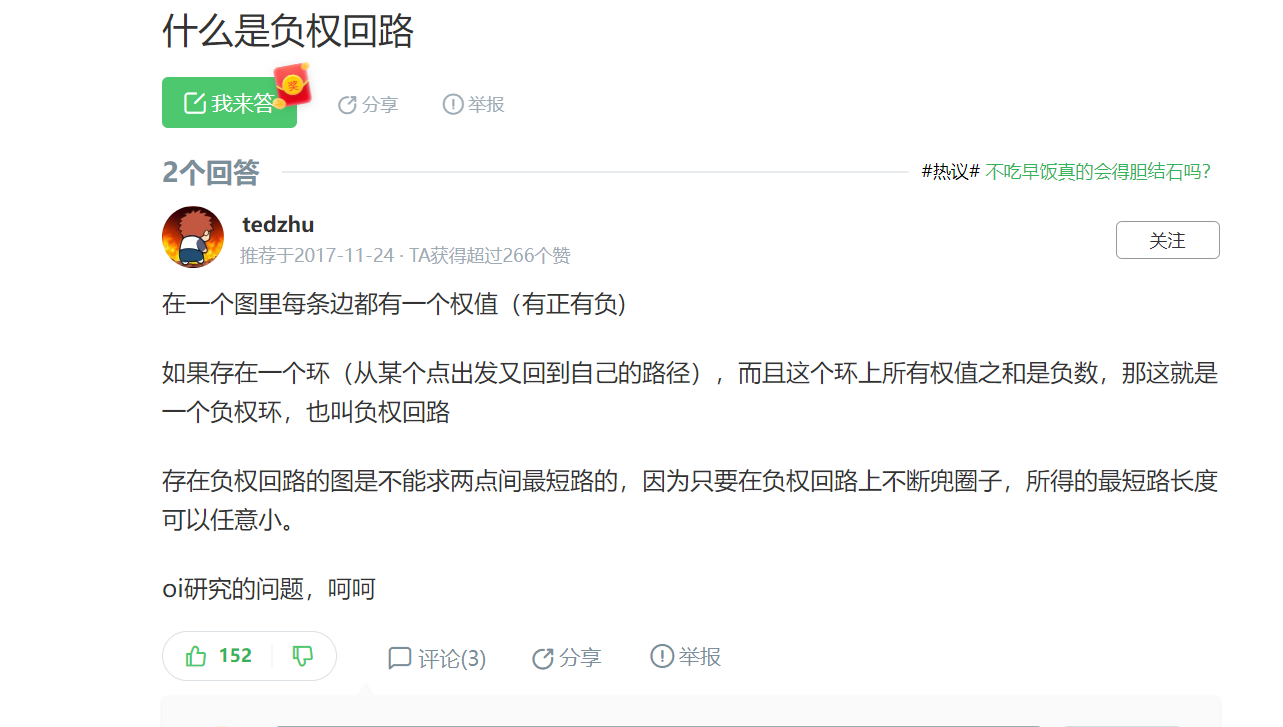
如果有负权回路的话，最短路不一定存在了

bellman-ford是可以求出是否有负环的,但平时不用，时间复杂度太高，后面SPFA会用到

鸽巢（抽屉）原理

Spfa
多源汇最短路
Floyd

4.第四章 数学知识（12.10）

进制转换

（要很熟练）

转换成10进制用的秦九韶算法，迭代方式提升效率

位运算

洛谷 P1469 找筷子

#include<bits/stdc++.h>
using namespace std;
//交换律 结合律 把偶数的先结合成0，最后只剩落单的和0异或还是它自己
int ans,n,a;//ans是所有数异或之后的结果，也就是题目所求的落单的筷子的数目

int main()
{
	cin>>n;
	for (int i=1;i<=n;i++)
	{
   	  	scanf("%d",&a);
		ans^=a;//把所有的数都异或起来
	}
	printf("%d",ans);
	return 0;
}

加法原理与乘法原理

结果可能很大，要对指定数字取余数。不能全部乘完之后再取余数，因为中间结果可能会溢出。可以乘完一次就取一次余数。实际上，加法或者乘法都可以这样做：

(a+b+c)%k = ((a+b)%k + c)%k

(a * b * c) % k = ((ab)%k * c)%k

组合数问题

例题

洛谷 P2822 [NOIP2016 提高组] 组合数问题

| 同余定理，前面是除数，后面是被除数

杨辉三角的性质

#include<bits/stdc++.h>
using namespace std;
long long c[2010][2010];
int main(){
	int t,k,m,n;
	cin >> t >> k;
	//先设置一个杨辉三角
    for(int i = 0; i <= 2000; i ++){
		c[i][0] = c[i][i] = 1;
		for(int j= 1; j < i ; j ++)
            //加法计算可以在途中取余
			c[i][j] = (c[i-1][j] + c[i-1][j-1])%k;
	}
    
		while(t--){
			int ans = 0;
			cin >> n >> m;
			for(int i = 0; i <= n; i ++)
				for(int j = 0; j <= min(i,m); j ++)
					ans+=c[i][j] == 0;
		
			cout << ans << endl;
		}	
		return 0;
}

约数

例题 P2926 [USACO08DEC] Patting Heads S

未解决

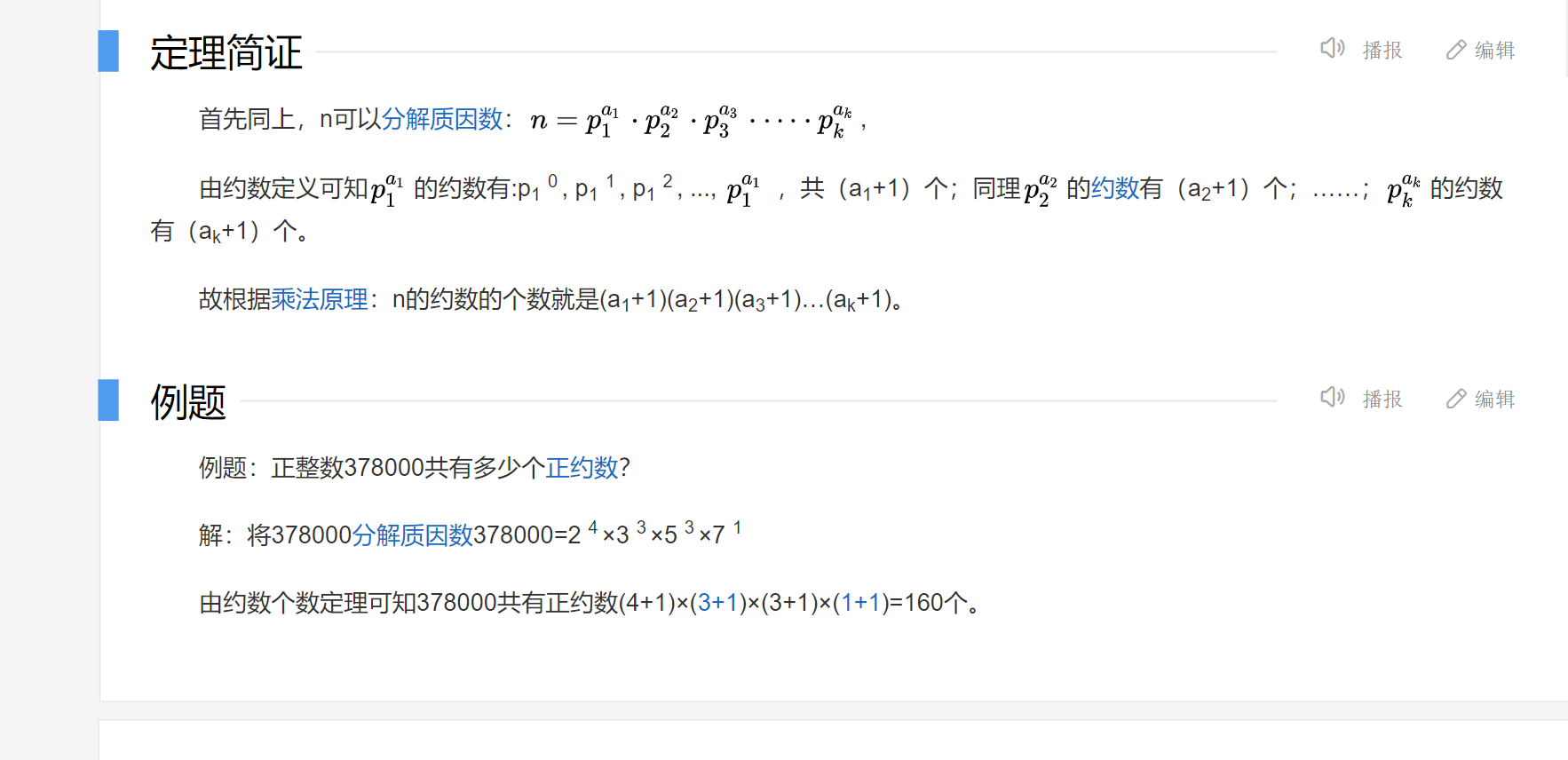
试除法求约数

约数个数和约数之和(两个公式)

约数个数证明：

质数和合数

所以，在以后的算法学习中，大家可以有意识地去使用线性筛进行解题，防止白给。除了这两种筛素数的方法，其实还有更加优秀的，时间复杂度低于O(N)的筛法，这里本人能力有限，就不进行介绍了，有兴趣的同学可以自己去查找相关资料。

埃氏筛

void get_primes1(){
    for(int i=2;i<=n;i++){
        if(!st[i]){
            primes[cnt++]=i;
            for(int j=i;j<=n;j+=i) st[j]=true;//可以用质数就把所有的合数都筛掉；
        }
    }
}

线性筛

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1000010;

//primes数组用来存放质数
int primes[N], cnt;
//st[i], i为质数则为false否则为true
bool st[N];

void get_primes(int n)
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i]) primes[cnt++] = i;
        //假设primes[0]为n最小的质因子,i为最大的因数，
        //易知若primes[i]中i>0,则会进入循环后产生多余的标记。
        for(int j = 0; primes[j] <= n / i; j ++)
        {
            //标记;primes[j]一定是primes[j]*i的最小质因子
            st[primes[j]*i] = true;
            //表明primes[j]一定是i的最小质因子,没有必要再遍历,primes要小于等于i的最小质因子
            //这样能保证每个数遍历一遍,而没有重复
            if(i % primes[j] == 0) break;
        }
    }
}

int main()
{
    int n;
    cin >> n;
    get_primes(n);
    cout << cnt << endl;
    return 0;
}

分解质因数

https://www.acwing.com/solution/content/9813/

#include<iostream>
#include<algorithm>
using namespace std;
int main(void)
{
    int n;cin>>n;
    while(n--)
    {
        int a;cin>>a;
        for(int i=2;i<=a/i;i++)
        {
            if(a%i==0)
            {
                int s=0;
                while(a%i==0)
                {
                    a/=i;
                    s++;
                }
                cout<<i<<" "<<s<<endl;  
            }

        }
        if(a>1) cout<<a<<' '<<1<<endl; ///
        cout<<endl;
    }
return 0;    
}

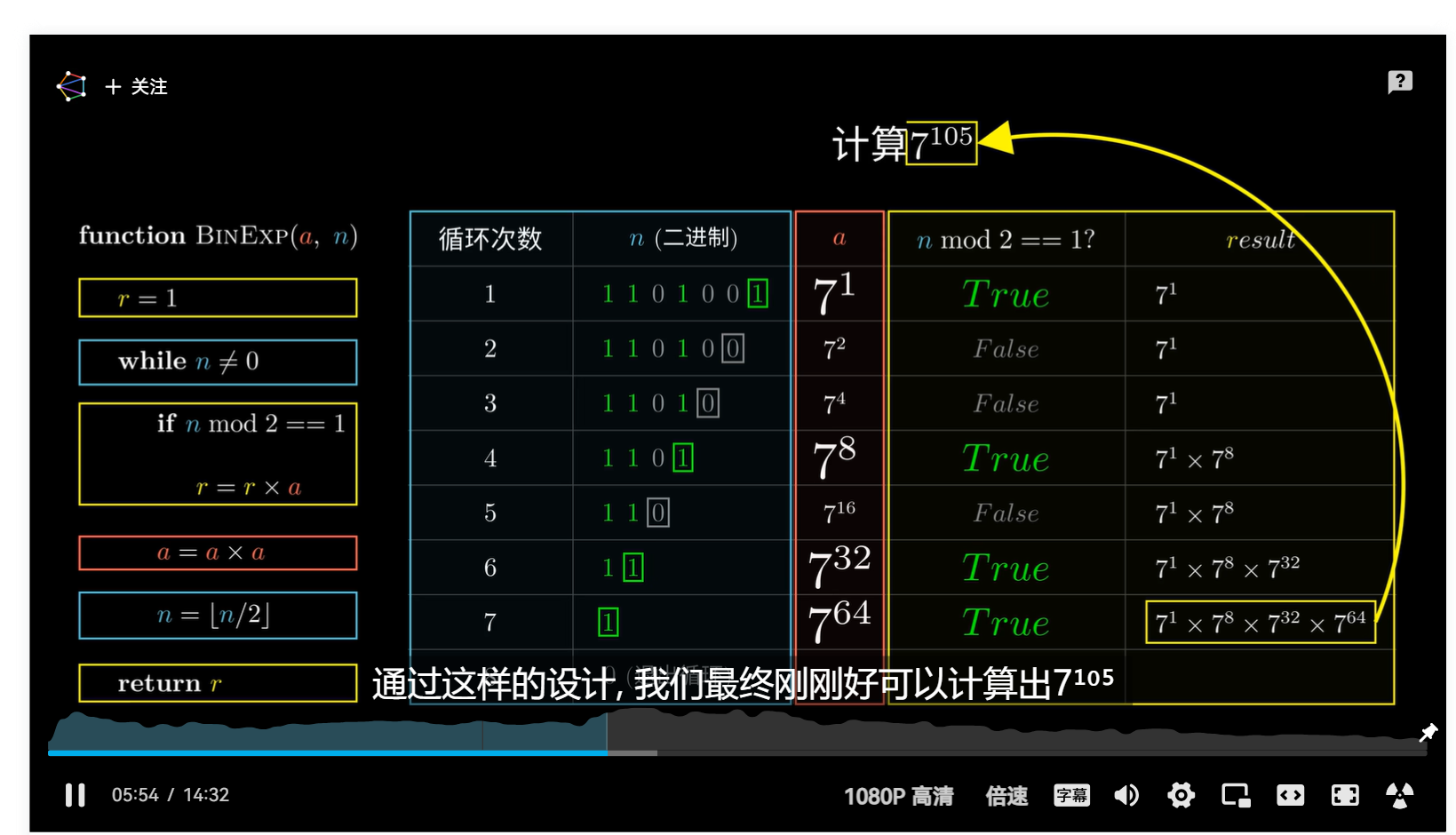
快速幂

https://blog.csdn.net/m0_52072919/article/details/116400820?ops_request_misc=&request_id=&biz_id=102&utm_term=%E5%BF%AB%E9%80%9F%E5%B9%82&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-116400820.nonecase&spm=1018.2226.3001.4187

这个博客很好

模板

https://www.acwing.com/problem/content/description/877/

#include<bits/stdc++.h>
using namespace std;
int n;
long long int qmi(long long int base, long long int power, long long int p)
{
	long long int result = 1;   
	while (power > 0)           
	{
		if (power & 1)         							
			result = result * base % p;   
			//根据公式每个项都取余数后在再做累乘
		base = base * base % p ;   
			//根据公式每个项都取余数后在再做平方操作      						
		power >>= 1;         						
	}
			//根据公式在最后的的结果上再来一次取余数
	return result % p;       
}
int main(){
    cin >> n;
    while(n --){
        int base,power,p;
        cin >> base >> power >> p;
        cout << qmi(base,power,p)<<endl;
    }
    return 0;
}

n mod 2可以写成n & 1, n/2 可以写成 n >> 1

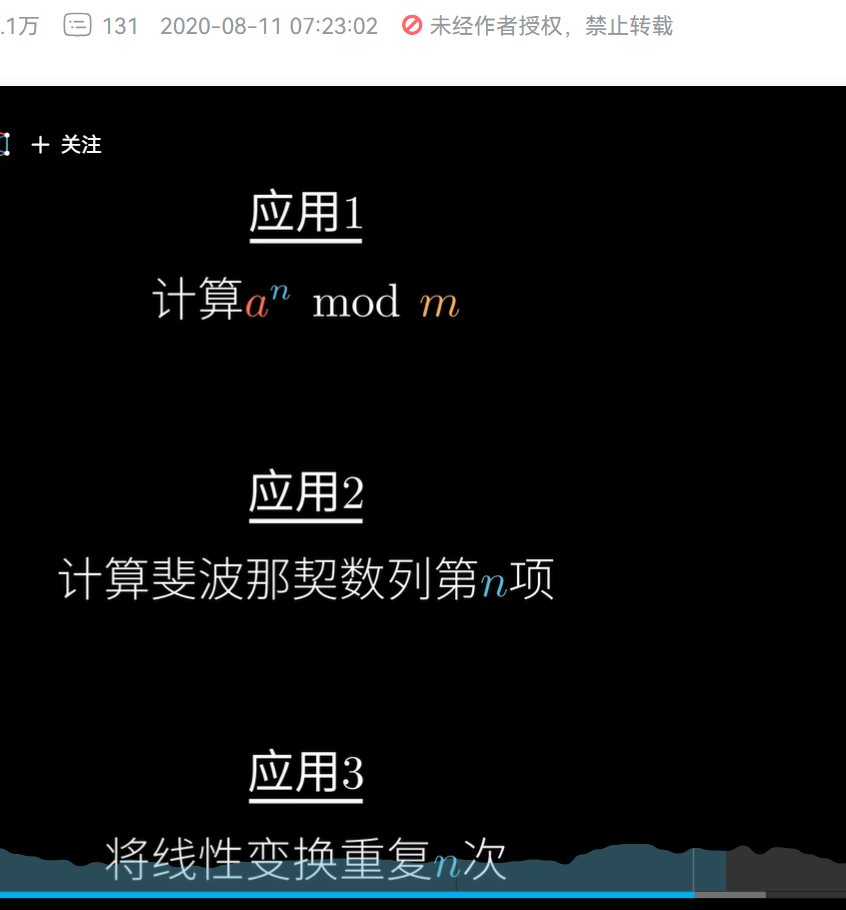
应用

欧拉（Euler）函数

https://www.acwing.com/solution/content/62556/

证明可用容斥原理

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
    ll k;cin>>k;
    while(k--)
    {
        ll x;
        cin>>x;
        ll res=x;
        for(ll i=2;i<=x/i;i++)
            if(x%i==0)
            {
                while(x%i==0)x/=i;
                res=res/i*(i-1);   //注意先除再乘  N/pk*(pk-1); 
            }
        if(x>1)res=res/x*(x-1);
        cout<<res<<endl;
    }
 }

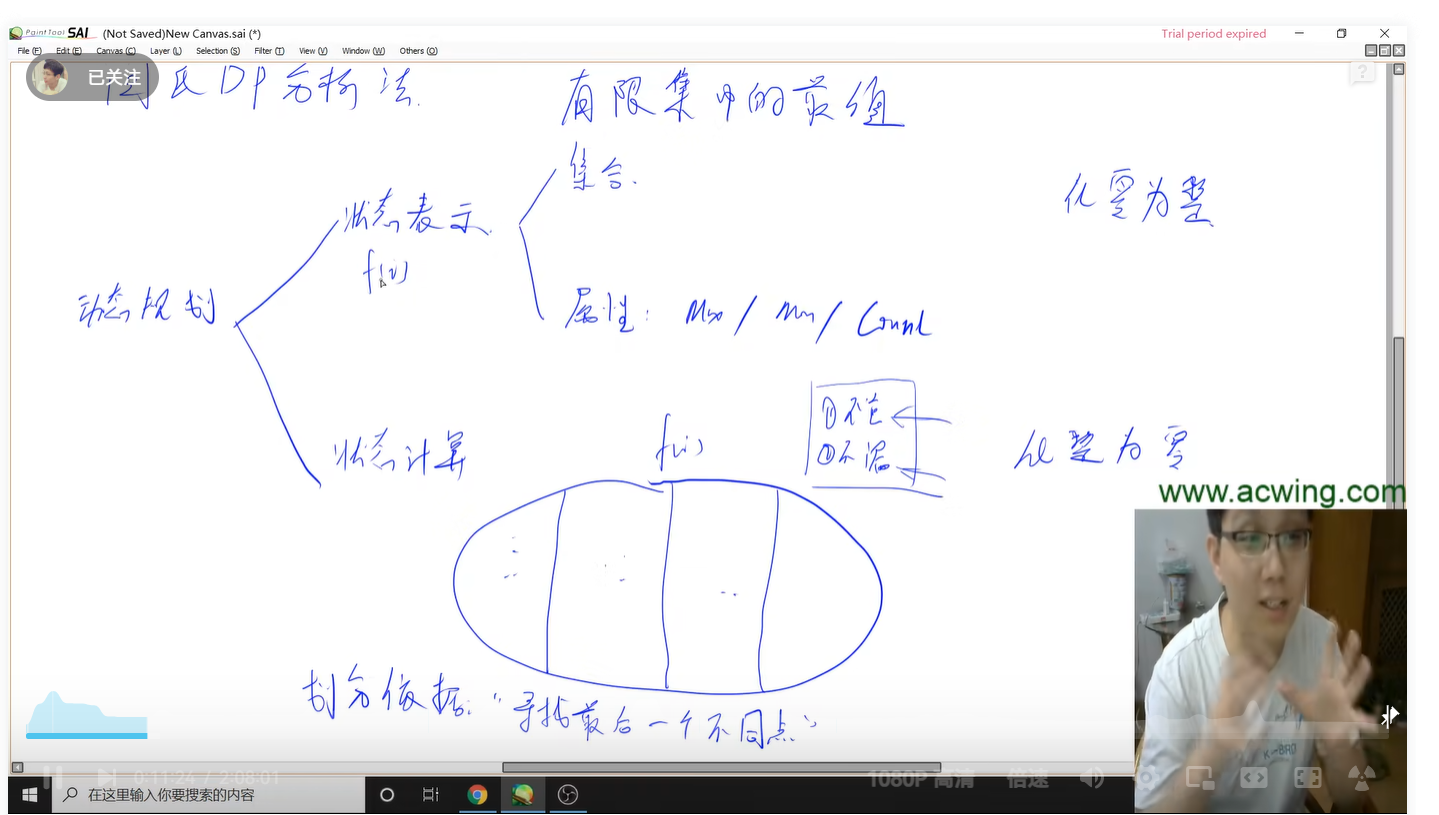
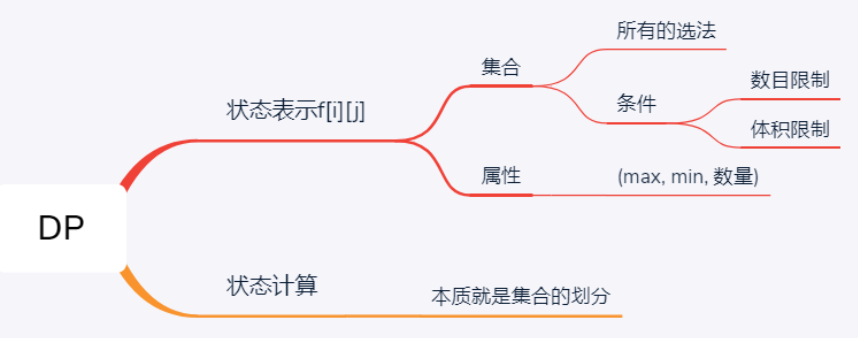
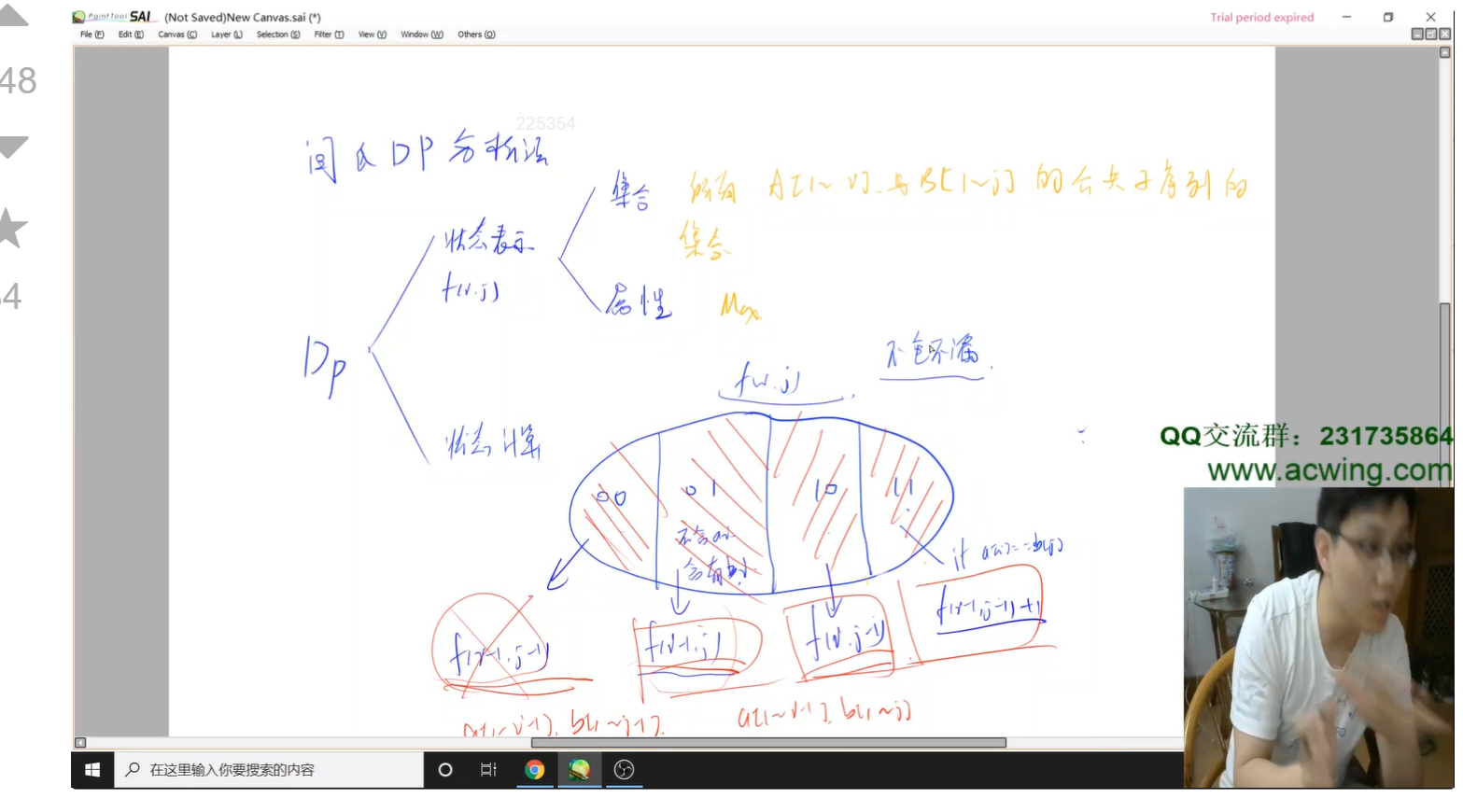
5.第五章 动态规划

闫式DP分析法

从集合角度分析DP问题，求有限集合的最值/个数..

状态表示：每次划分一个子集 （化零为整） —多做题，刚开始的时候很难想到如何表示，做过类似的题才能大概率写出来

属性：存的是什么东西,max/min/count之类的

状态计算:化整为零

f[i]的子集，不重复，不遗漏(f[i]的全部都被包含),比如取最大值，给每个子集的最大值取个max。

集合划分的套路：寻找最后一个不同点

想学好dp整理好模型很重要，比如选择问题-背包模型，子序列问题-最长上升子序列这种模型

dp很看重经验，(做过类似的题)

image-20240116203838110

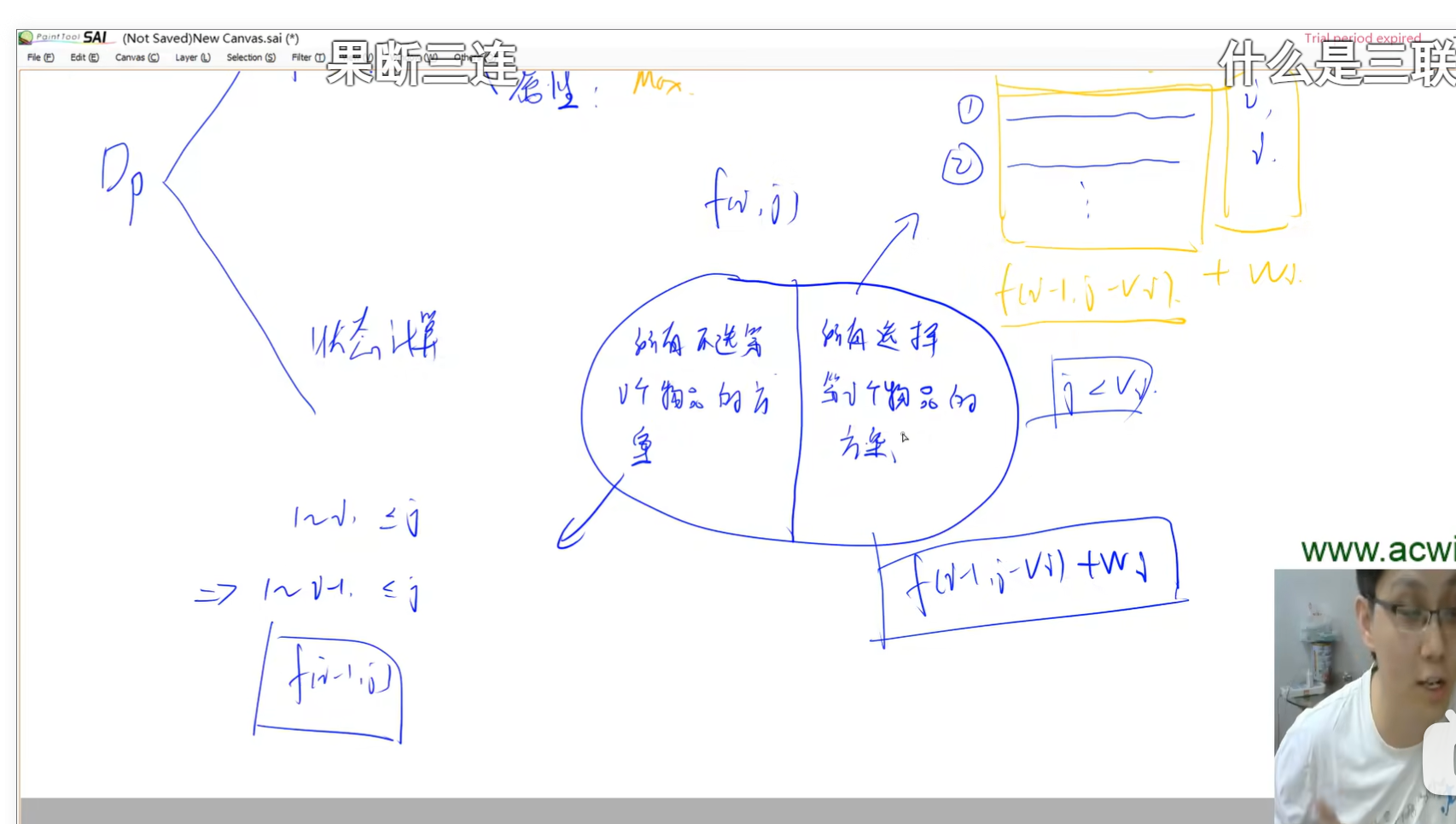
状态表示 f[i,j]

选择物品i的方案不一定存在，要判断j 是否>=v[i]

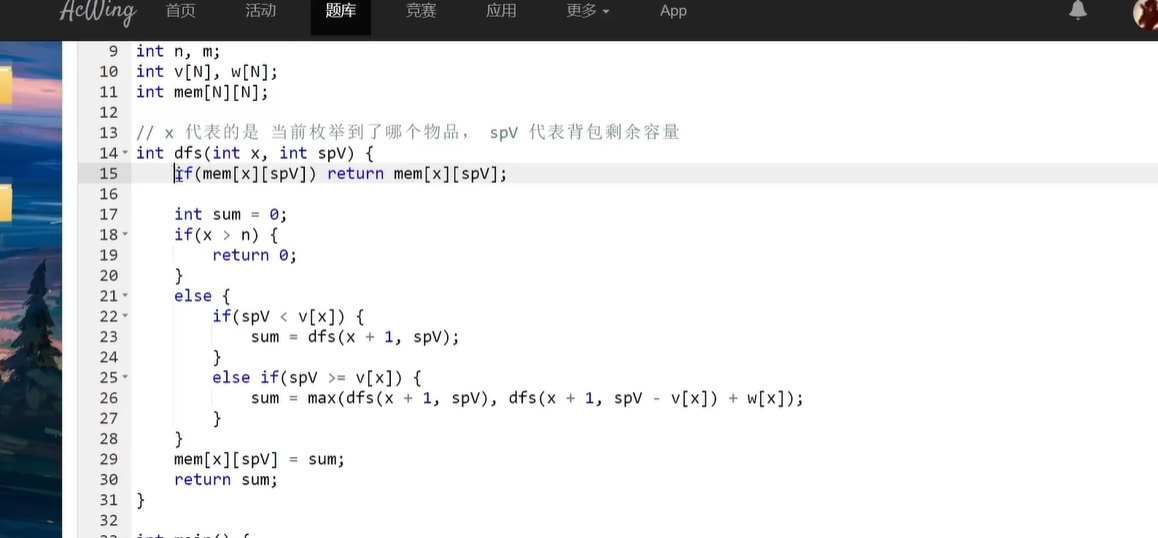
例题 https://www.acwing.com/problem/content/1214/ 地宫取宝

重复调用的问题适合改动态规划

斐波那契数列优化

1.递归

2.记忆化

3.dp

4.使用两个变量

动态规划就是递推的子集

例题

image-20231221194259987

背包问题

01背包问题

一维 01 逆序，完全 正序

记化化搜索

二维DP

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 1005;
int v[MAXN];    // 体积
int w[MAXN];    // 价值 
int f[MAXN][MAXN];  // f[i][j], j体积下前i个物品的最大价值 

int main() 
{
    int n, m;   
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           

    cout << f[n][m] << endl;

    return 0;
}

滚动数组（优化成一维DP）版本

for(int i = 1; i <= n; i++) 
    //这里如果从0~m的话，可能会用到上层被这层覆盖的值
   //可以自己画表
    for(int j = m; j >= 0; j--)
    {
        if(j < v[i]) 
            f[i][j] = f[i - 1][j];  // 优化前
            f[j] = f[j];            // 优化后，该行自动成立，可省略。
        else    
            f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);  // 优化前
            f[j] = max(f[j], f[j - v[i]] + w[i]);                   // 优化后



完全背包

二维

#include<bits/stdc++.h>
using namespace std;
const int P = 1e3 + 10;
int N,V;
int v[P],w[P];
int mm[P][P];
// int dfs(int x,int spV){
//     if(x > N || spV < 0)mm[x][spV] = 0;
//     else if(spV < v[x]) mm[x][spV]=dfs(x+1,spV);
//   return mm[x][spV];
//             else mm[x][spV] = max(dfs(x + 1,spV),dfs(x,spV-v[x])+w[x]);
  
// }
int main(){
    cin >> N >> V;
    for(int i = 1; i <= N; i ++){
        cin >> v[i] >> w[i];
    }
    // int res = dfs(1,V);
    for(int i = 1; i <= N; i ++){
        for(int j = 1; j <= V; j ++){
            if(j < v[i])mm[i][j] = mm[i - 1][j];
    else mm[i][j] = max(mm[i - 1][j],mm[i][j - v[i]]+ w[i]);
        }
    }
    cout << mm[N][V];
    return 0;
}

//二维正序枚举，下面的写法不舒服，可以把上面的改成正序的
#include<iostream>
using namespace std;
const int N = 1010;
int f[N][N];
int v[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++)
    {
        cin>>v[i]>>w[i];
    }

    for(int i = 1 ; i<=n ;i++)
    for(int j = 0 ; j<=m ;j++)
    {
        for(int k = 0 ; k*v[i]<=j ; k++)
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
    }

    cout<<f[n][m]<<endl;
}

一维

可以画图，体积从正序枚举是对的，每个物品可以无限取，从倒序枚举是错的，不然和01（只能取一次）一样了，画个图就ok

#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++)
    {
        cin>>v[i]>>w[i];
    }

for(int i = 1 ; i<=n ;i++)
    //j小于v[i]的不改变
for(int j = v[i] ; j<=m ;j++)
{
        f[j] = max(f[j],f[j-v[i]]+w[i]);
}
	cout<<f[m]<<endl;

}

多重背包

多重背包问题 I (数据范围100，n^3没超1e7-1e8)

https://www.acwing.com/problem/content/4/

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 110;

int v[N], w[N], s[N];
int f[N][N];
int n, m;

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i] >> s[i];

for(int i = 1; i <= n; i ++){//枚举背包
    for(int j = 1; j <= m; j ++){//枚举体积
        //k从0开始，可能一个都不选
        for(int k = 0; k <= s[i]; k ++){
            if(j >=  k * v[i]){
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
            }
        }
    }
}

cout << f[n][m] << endl;

return 0;

}

多重背包问题 II (正常做会超)

https://www.acwing.com/problem/content/5/

分组背包

二维
#include<bits/stdc++.h>
using namespace std;

const int N=110;
int f[N][N];  //只从前i组物品中选，当前体积小于等于j的最大值
int v[N][N],w[N][N],s[N];   //v为体积，w为价值，s代表第i组物品的个数
int n,m,k;

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>s[i];
        for(int j=0;j<s[i];j++){
            cin>>v[i][j]>>w[i][j];  //读入
        }
    }

for(int i=1;i<=n;i++){
    for(int j=0;j<=m;j++){
        f[i][j]=f[i-1][j];  //不选
        for(int k=0;k<s[i];k++){
            if(j>=v[i][k])     f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);  
        }
    }
}
cout<<f[n][m]<<endl;
}
一维
因为只用到了第i-1列，所以可以仿照01背包的套路逆向枚举体积
#include<bits/stdc++.h>
using namespace std;

const int N=110;
int f[N];
int v[N][N],w[N][N],s[N];
int n,m,k;

int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        cin>>s[i];
        for(int j=0;j<s[i];j++){
            cin>>v[i][j]>>w[i][j];
        }
    }

for(int i=0;i<n;i++){
    for(int j=m;j>=0;j--){
        for(int k=0;k<s[i];k++){    //for(int k=s[i];k>=1;k--)也可以
            if(j>=v[i][k])     f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);  
        }
    }
}
cout<<f[m]<<endl;

}

二维费用背包

例题 洛谷 1130红牌

例题 https://www.acwing.com/problem/content/description/8/

背包问题的变种

01背包求方案数

例题 acwing278. 数字组合

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
int n,m;
int a[N];
int f[N][N];
/*int dfs(int u,int spSum){
	if(f[u][spSum]!=0)return f[u][spSum];
	else if(spSum != 0 && u > n)f[u][spSum] = 0;
	else if(spSum < 0)f[u][spSum] = 0;
	else if(spSum == 0)f[u][spSum] = 1;
	else f[u][spSum] = dfs(u +1,spSum) + dfs(u + 1,spSum - a[u]);
	return f[u][spSum];
}*/

int main(){

	cin >> n >>m;
	for(int i = 1; i <= n; i ++){
		cin >> a[i];
	}
    
	for (int i = 0; i <= n+1; i++) {
        f[i][0] = 1;  // 当和为0时，方案数为1
    }
    for (int i = n; i >= 1; i--) {
        for (int j = 1; j <= m; j++) {
            f[i][j] = f[i + 1][j];  // 不选择第i个数
            if (j >= a[i]) {
                f[i][j] += f[i + 1][j - a[i]];  // 选择第i个数
            }
        }
    }
    cout << f[1][m];
	return 0;
}
01背包求具体方案

为什么逆序枚举？

https://www.acwing.com/problem/content/description/12/

https://blog.csdn.net/yl_puyu/article/details/109960323解释很好

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1005;

int n, m;
int v[N], w[N];
int f[N][N]; 

int main() {
    cin >> n >> m;
    
    for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
    
    for (int i = n; i >= 1; --i) 
        for (int j = 0; j <= m; ++j) {
            f[i][j] = f[i + 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }
    
    // 在此，f[1][m]就是最大数量
    int j = m;
    for (int i = 1; i <= n; ++i) 
        if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) {
            cout << i << ' ';
            j -= v[i];
        }
    return 0;
}

01背包求最优方案数

背包例题

https://www.luogu.com.cn/paste/s2v5pn69

洛谷P1802 5倍经验日（01背包变形问题）

这是一道变了形的01背包

首先我们因为和每个人打都一定有经验所以一定都要打一遍。

所以不难想到max=lose[1]+lose[2]......+lose[n]+某些磕了药打赢的多出的经验值

因此我们可以进行一个转换，把价值记为win[i]-lose[i]，溶剂就是要打赢磕的药，然后要使价值总和最大，然后就变成了基础的零一背包了。。。

#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<cstdio>
using namespace std;
int a[100005];
long long f[1000005];
int win[100005];
int v[100005];
int lose[100005];
int main()
{
    int n,m;
    int sum=0;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++){
        scanf("%d%d%d",&lose[i],&win[i],&v[i]);
        a[i]=win[i]-lose[i];
        sum=sum+lose[i];
    }
    for (int i=1;i<=n;i++){
        for (int j=m;j>=v[i];j--){
            f[j]=max(f[j],f[j-v[i]]+a[i]);
        }
    }
    printf("%lld",5*(f[m]+sum));
    return 0;
}
完全背包求方案数

例题

https://www.acwing.com/problem/content/description/1373/

题解：https://www.acwing.com/solution/content/31275/

//和01背包求方案数写法除了改循环条件几乎没区别

https://www.acwing.com/problem/content/description/3385/

背包例题

https://www.luogu.com.cn/paste/s2v5pn69

洛谷P1802 5倍经验日（01背包变形问题）
这是一道变了形的01背包

首先我们因为和每个人打都一定有经验所以一定都要打一遍。

所以不难想到max=lose[1]+lose[2]......+lose[n]+某些磕了药打赢的多出的经验值

因此我们可以进行一个转换，把价值记为win[i]-lose[i]，溶剂就是要打赢磕的药，然后要使价值总和最大，然后就变成了基础的零一背包了。。。

#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<cstdio>
using namespace std;
int a[100005];
long long f[1000005];
int win[100005];
int v[100005];
int lose[100005];
int main()
{
    int n,m;
    int sum=0;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++){
        scanf("%d%d%d",&lose[i],&win[i],&v[i]);
        a[i]=win[i]-lose[i];
        sum=sum+lose[i];
    }
    for (int i=1;i<=n;i++){
        for (int j=m;j>=v[i];j--){
            f[j]=max(f[j],f[j-v[i]]+a[i]);
        }
    }
    printf("%lld",5*(f[m]+sum));
    return 0;
}

区间DP

例题 石子合并 https://www.acwing.com/problem/content/description/284/

视频讲解的很好

绝大部分区间dp问题，先枚举区间长度，再枚举区间左端点

状态机DP

https://blog.csdn.net/qq_42958831/article/details/130059756

这个博客把灵神的思路讲得很明白

https://www.acwing.com/problem/content/description/1059/

题解讲得很好

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10, M = 110;

int n, k;
int w[N];
int f[N][M][2];

int main()
{
    cin >> n >> k;
    for (int i = 1; i <= n; ++ i) cin >> w[i];

    memset(f, -0x3f, sizeof f);
    f[0][0][0] = 0; //初始状态f[0][0][0]

    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j <= k; ++ j)
        {
            f[i][j][0] = f[i - 1][j][0];
            if (j) f[i][j][0] = max(f[i][j][0], f[i - 1][j - 1][1] + w[i]);
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j][0] - w[i]);
        }
    }

    int res = 0;
    for (int j = 0; j <= k; ++ j) res = max(res, f[n][j][0]); //目标状态f[n][j][0]

    cout << res << endl;

    return 0;
}


https://www.acwing.com/problem/content/1058/

#include<bits/stdc++.h>
using namespace std;
const int A =1e5,B = 10,C = 2, inf = 0x3f3f3f;
int dp[A][B][C];
int w[A];
int main(){
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++){
        cin >> w[i]; 
    }
    // dp[0][2][0] = 0;
    // dp[0][2][1] = -inf;
    memset(dp, -0x3f, sizeof dp);
    for(int i = 0; i <= 2; ++ i) dp[0][i][0] = 0;
    for(int i = 1; i <= n; i ++){
        for(int j = 0; j <= 2; j ++){
            dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j][1] + w[i]);
            dp[i][j][1] = dp[i - 1][j][1];
            if(j)dp[i][j][1] = max(dp[i][j][1], dp[i - 1][j - 1][0] - w[i]);

        }
    }
    int ans = 0;
    for(int i = 0; i <= 2; i ++){
        ans = max(dp[n][i][0],ans);
    }
    cout << ans;
}

树形DP

https://www.bilibili.com/video/BV17o4y187h1/?spm_id_from=333.337.search-card.all.click&vd_source=4452cbcad134fb17ec9cfb03a0acbdac 树的直径讲解

例题见视频下方链接

https://www.cnblogs.com/RioTian/p/15163878.html 博客

卡特兰数

https://leetcode.cn/circle/discuss/lWYCzv/

例题1 进出栈序列

线性DP

最长上升子序列I

算法1
(动态规划) O(n2)

状态表示：f[i]表示从第一个数字开始算，以w[i]结尾的最大的上升序列。(以w[i]结尾的所有上升序列中属性为最大值的那一个)

状态计算（集合划分）：j∈(0,1,2,..,i-1), 在w[i] > w[j]时，
f[i] = max(f[i], f[j] + 1)。
有一个边界，若前面没有比i小的，f[i]为1（自己为结尾）。

最后在找f[i]的最大值。

时间复杂度
O(n2)
状态数(n) * 转移数(n)

#include <iostream>

using namespace std;

const int N = 1010;

int n;
int w[N], f[N];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) cin >> w[i];

    int mx = 1;    // 找出所计算的f[i]之中的最大值，边算边找
    for (int i = 0; i < n; i++) {
        f[i] = 1;    // 设f[i]默认为1，找不到前面数字小于自己的时候就为1
        for (int j = 0; j < i; j++) {
            if (w[i] > w[j]) f[i] = max(f[i], f[j] + 1);    // 前一个小于自己的数结尾的最大上升子序列加上自己，即+1
        }
        mx = max(mx, f[i]);
    }

    cout << mx << endl;
    return 0;
}

算法2
(动态规划 + 二分) O(nlogn)

我认为可以延伸到求满足某个性质的一个子序列

最长上升子序列II （数据范围n<1e5）

这题解法特别好

https://www.acwing.com/solution/content/2192/ 题解讲得很清楚
例题：蓝桥杯 接龙序列

最长公共子序列

状态计算可能有重复，只要不越界不遗漏就ok

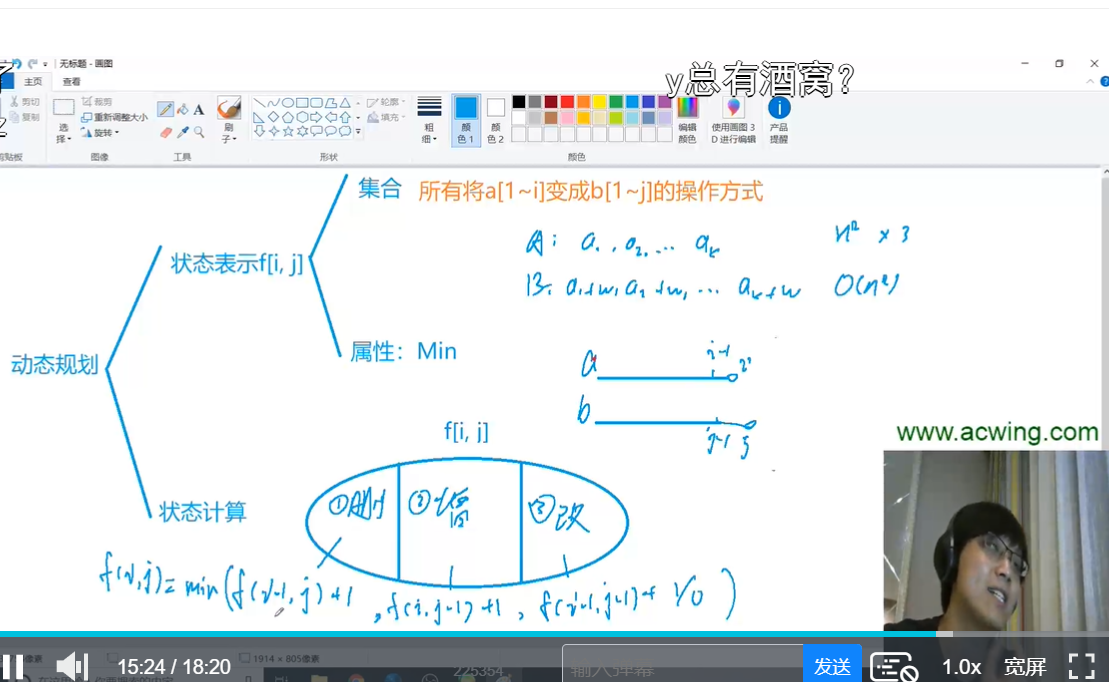
编辑距离

有f[i-1]基本i都要从1开始遍历

https://www.acwing.com/activity/content/problem/content/1094/

状态压缩DP

例题 https://www.luogu.com.cn/problem/P8687

图上动态规划

日期问题

https://blog.51cto.com/u_15656645/5373606 蓝桥 日期问题模板

闰年要被4整除并且不能被100整除或者能被400整除

(year % 4 == 0 && year % 100 != 0 )||(year % 400 == 0)

https://www.acwing.com/activity/content/problem/content/9436/

https://www.acwing.com/blog/content/24163/题解大合集

https://www.acwing.com/solution/content/37448/ 这个代码的流程很好，可以当模板

贡献法

https://blog.csdn.net/weixin_46239370/article/details/115262482 蓝桥杯 子串分值和 用到乘法原理和贡献法，题解很好